
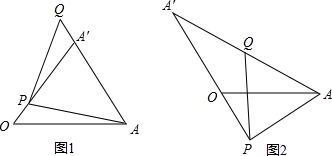
分析 (1)截取A′D=PA′,先证得△OAA′是正三角形,△PA′D是正三角形,进而证得△QPA′≌△APD,得出QA′=DA,即可证得A′D+DA=PA′+QA′=AA′=OA;
(2)作OC⊥AA′于C,则AC=A′C,根据已知条件证得$\frac{AA′}{OA′}$=$\sqrt{3}$,然后作PD∥OA,交A′A的延长线于D,进而证得△PAA′≌△PQD,得出AA′=DQ,A′Q=AD,根据平行线分线段成比例定理求得$\frac{AA′}{OA′}$=$\frac{AD}{OP}$=$\sqrt{3}$,得出OP=$\frac{\sqrt{3}}{3}$AQ′,即可得出PA′、QA′、OA之间满足的数量关系为PA′=$\frac{{\sqrt{3}}}{3}$QA′+OA.
(3)由(2)可知$\frac{AA′}{OA′}$=$\sqrt{3}$,得出AA′=4$\sqrt{3}$,A′Q=AQ=2$\sqrt{3}$,由OP=$\frac{\sqrt{3}}{3}$AQ′,得出OP=2,PA′=4+2=6,作QE⊥PA′于E,解直角三角形求得A′E=$\frac{\sqrt{3}}{2}$A′Q=3,从而求得A′E=PE,得出△PQA′是等腰三角形,得出∠PQA=60°,即可证得△PAQ是等边三角形,然后解直角三角形即可求得.
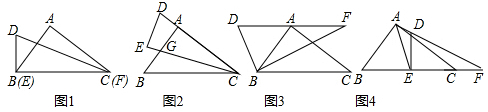
解答 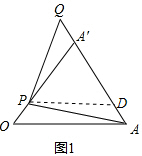 解:(1)如图1,截取A′D=PA′,
解:(1)如图1,截取A′D=PA′,
∵线段OA绕点O逆时针旋得到∠AOA′,
∴OA=OA′,
∵∠AOA′=60°,
∴OA=OA′=AA′,∠OA′A=60°,
∴△OAA′是正三角形,△PA′D是正三角形,
∴A′D=PA′=PD,∠A′PD=∠A′DP=60°,
∵PQ=PA,
∴∠Q=∠PAA′,
∵∠Q+∠QPA′=60°,∠PAA′+∠APD=60°,
∴∠QPA′=∠APD,
在△QPA和△APD中,
$\left\{\begin{array}{l}{∠Q=∠PAA′}\\{PQ=PA}\\{∠QPA′=∠APD}\end{array}\right.$
∴△QPA′≌△APD(ASA),
∴QA′=DA,
∴A′D+DA=PA′+QA′=AA′,
∴PA′+QA′=OA;
(2)如图2,∵∠AOA′=120°,OA=OA′,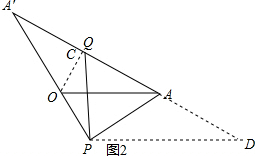
∴∠OAA′=∠A′=30°,
作OC⊥AA′于C,则AC=A′C
AC=$\frac{\sqrt{3}}{2}$OA,
∴$\frac{A′C}{OA′}$=$\frac{\sqrt{3}}{2}$,
∴$\frac{AA′}{OA′}$=$\sqrt{3}$,
作PD∥OA,交A′A的延长线于D,
∴∠D=∠OAA′=∠A′=30°,
∴PA′=PD,
∵PA=PQ,
∴∠PAQ=∠PQA,
在△PAA′和△PQD中,
$\left\{\begin{array}{l}{∠D=∠A′}\\{∠PAQ=∠PQA}\\{PQ=PA}\end{array}\right.$,
∴△PAA′≌△PQD(AAS),
∴AA′=DQ,
∴A′Q=AD,
∵PD∥OA,
∴$\frac{AA′}{OA′}$=$\frac{AD}{OP}$=$\sqrt{3}$,
∵AD=A′Q,
∴$\frac{A′Q}{OP}$=$\sqrt{3}$,
∴OP=$\frac{\sqrt{3}}{3}$AQ′,
∴线段PA′、QA′、OA之间满足的数量关系为PA′=OP+OA′=$\frac{{\sqrt{3}}}{3}$QA′+OA.
故答案为PA′=$\frac{{\sqrt{3}}}{3}$QA′+OA.
(3)如图3,由(2)可知$\frac{AA′}{OA′}$=$\sqrt{3}$,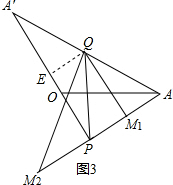
∴AA′=4$\sqrt{3}$,
∵Q为AA′的中点,
∴A′Q=AQ=2$\sqrt{3}$,
∵OP=$\frac{\sqrt{3}}{3}$AQ′,
∴OP=2,
∴PA′=4+2=6,
作QE⊥PA′于E,
∵∠A′=30°,
∴A′E=$\frac{\sqrt{3}}{2}$A′Q=3,
∴A′E=PE,
∴A′Q=PQ=2$\sqrt{3}$,
∴∠A′=∠QPA′=30°,
∴∠PQA=60°,
∵PQ=PA,
∴△PQA是等边三角形,
∵∠PQM1=30°,
∴QM1=$\frac{\sqrt{3}}{2}$PQ=$\frac{\sqrt{3}}{2}$×2$\sqrt{3}$=3,
∵∠PQM2=30°,∠PQA=∠PAQ=60°,
∴∠AQM2=90°,
∴QM=$\sqrt{3}$AQ=$\sqrt{3}$×$2\sqrt{3}$=6.
∴QM的长为3或6.
点评 本题考查了旋转的性质,等边三角形的判定和性质,等腰三角形的判定和性质,平行线的性质,三角形全等的判定和性质以及解直角三角形等,熟练掌握性质和定理是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2016-2017学年浙江省衢州市八年级下学期第一次月考数学试卷(解析版) 题型:单选题
下列一元二次方程有两个相等的实数根的是( )
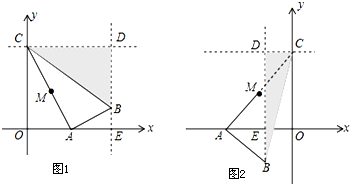
A. x2+1=0 B. x2+4x﹣4=0 C. x2+x+ =0 D. x2﹣x+
=0 D. x2﹣x+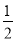 =0
=0
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
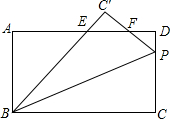 如图所示,矩形ABCD中,AB=6,BC=10,将矩形ABCD沿着过点B的直线折叠,使得点C落在点C′处,折痕所在直线与CD相交于点P,BC′与AD相交于点E,PC′与AD相交于点F,若△C′EF≌△DPF,则PC的长为$\frac{30}{7}$.
如图所示,矩形ABCD中,AB=6,BC=10,将矩形ABCD沿着过点B的直线折叠,使得点C落在点C′处,折痕所在直线与CD相交于点P,BC′与AD相交于点E,PC′与AD相交于点F,若△C′EF≌△DPF,则PC的长为$\frac{30}{7}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
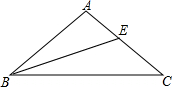 如图,在△ABC中,AB=AC,∠A=100°,BE平分∠ABC交AC于点E.
如图,在△ABC中,AB=AC,∠A=100°,BE平分∠ABC交AC于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com