
分析 (1)首先比较出每组两个数的平方的大小关系,然后判断出原来两个数的大小关系即可.
(2)首先比较出每组两个数的立方的大小关系,然后判断出原来两个数的大小关系即可.
(3)首先比较出每组两个数的六次方的大小关系,然后判断出原来两个数的大小关系即可.
(4)首先比较出每组两个数的平方的大小关系,然后判断出原来两个数的大小关系即可.
(5)首先判断出$\frac{3-\sqrt{15}}{2}$<0,即可判断出$\frac{3-\sqrt{15}}{2}$与$\frac{7}{8}$的大小关系.
解答 解:(1)${(\sqrt{6})}^{2}=6$,${(\frac{5}{2})}^{2}=\frac{25}{4}$,
∵6<$\frac{25}{4}$,
∴$\sqrt{6}$<$\frac{5}{2}$.
(2)${(\root{3}{20})}^{3}=20$,${(\frac{7}{2})}^{3}$=42.875,
∵20<42.875,
∴$\root{3}{20}$<$\frac{7}{2}$.
(3)${(\root{3}{3})}^{6}$=9,${(\sqrt{2})}^{6}=8$,
∵9>8,
∴$\root{3}{3}$>$\sqrt{2}$.
(4)${(\sqrt{41})}^{2}$=41,(6.23)2=38.8129,
∵41>38.829,
∴$\sqrt{41}$>6.23.
(5)∵$\frac{3-\sqrt{15}}{2}$<$\frac{3-3}{2}=0$,
∴$\frac{3-\sqrt{15}}{2}$<0,
∵$\frac{7}{8}>0$,
∴$\frac{3-\sqrt{15}}{2}$<$\frac{7}{8}$.
点评 此题主要考查了实数大小比较的方法,要熟练掌握,解答此题的关键是通过比较每组两个数的乘方的大小关系,判断出原来两个数的大小关系.


科目:初中数学 来源: 题型:解答题
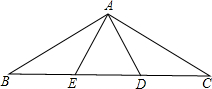 如图,AB=AC,∠BAC=120°,AD⊥AB,AE⊥AC.
如图,AB=AC,∠BAC=120°,AD⊥AB,AE⊥AC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com