练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在一次数学活动课上，张明用17个边长为1的小正方形搭成了一个几何体，然后他请王亮用其他同样的小正方体在旁边再搭一个几何体，使王亮所搭几何体恰好可以和张明所搭几何体拼成一个无缝隙的大长方体（不改变张明所搭几何体的形状），那么王亮至少还需要个小立方体，王亮所搭几何体的表面积为 ．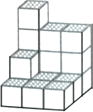

    【答案】19；48
    【解析】∵王亮所搭几何体恰好可以和张明所搭几何体拼成一个无缝隙的大长方体，
    ∴该长方体需要小立方体4×32=36个，
    ∵张明用17个边长为1的小正方形搭成了一个几何体，
    ∴王亮至少还需36﹣17=19个小立方体，
    表面积为：2×（9+7+8）=48．
    先确定张明所搭几何体所需的正方体的个数，在确定两人共搭建几何体所需小立方体的数量，求差即可．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中，若一图形各点的纵坐标不变，横坐标分别减5，那么图形与原图形相比（ ）
    A.向右平移了5个单位长度
    B.向左平移了5个单位长度
    C.向上平移了5个单位长度
    D.向下平移了5个单位长度

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小明做了以下5道题：①（x﹣1）（x+4）=x2﹣4；②（﹣3+x）（3+x）=x2﹣9；③（﹣5x+7y）（﹣5x﹣7y）=25x2﹣49y2；④（xy﹣6）2=x2y2﹣12xy+36；⑤（﹣x﹣y）2=x2+2xy+y2 ， 你认为小明一共做对了（ ）
    A.5道
    B.4道
    C.3道
    D.2道

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某商店销售10台A型和20台B型电脑的利润为4000元，销售20台A型和10台B型电脑的利润为3500元.

    （1）求每台A型电脑和B型电脑的销售利润；

    （2）该商店计划一次购进两种型号的电脑共100台，其中B型电脑的进货量不超过A型电脑的2倍，设购进A型电脑x台，这100台电脑的销售总利润为y元.

    ①求y关于x的函数关系式；

    ②该商店购进A型、B型电脑各多少台，才能使销售总利润最大？

    （3）实际进货时，厂家对A型电脑出厂价下调m(0<m<100)元，且限定商店最多购进A型电脑70台.若商店保持两种电脑的售价不变，请你根据以上信息及(2)中条件，设计出使这100台电脑销售总利润最大的进货方案.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】餐桌边的一蔬一饭，舌尖上的一饮一酌，实属来之不易，舌尖上的浪费让人触目惊心．据统计，中国每年浪费的食物总量折合粮食约500亿千克，这个数据用科学记数法表示为（ ）

    A．5×109千克 B．50×109千克

    C．5×1010千克 D．0.5×1011千克

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列计算正确的是（　　）

    A. ﹣3（a+b）＝﹣3a+3b B. 2（x+12y）＝2x+12y

    C. x3+2x5＝3x8 D. ﹣x3+3x3＝2x3

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】边长都为整数的△ABC≌△DEF ,AB与DE是对应边，AB=2，BC=4,若△DEF的周长为偶数，则 DF的取值为（ ）
    A.3
    B.4
    C.5
    D.3或4或5

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读理解：运用“同一图形的面积相等”可以证明一些含有线段的等式成立，这种解决问题的方法我们称之为面积法. 如图1，在等腰△ABC中，AB=AC， AC边上的高为h，点M为底边BC上的任意一点，点M到腰AB、AC的距离分别为h1、h2，连接AM，利用S△ABC=S△ABM＋S△ACM，可以得出结论：h= h1＋h2.

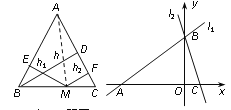
    类比探究：在图1中，当点M在BC的延长线上时，猜想h、h1、h2之间的数量关系并证明你的结论.

    拓展应用：如图2，在平面直角坐标系中，有两条直线l1：y =x+3，l2：y =－3x+3，若l2上一点M到l1的距离是1，试运用 “阅读理解”和“类比探究”中获得的结论，求出点M的坐标.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，一居民楼底部B与山脚P位于同一水平线上，小李在P处测得居民楼顶A的仰角为60°，然后他从P处沿坡角为45°的山坡向上走到C处，这时，PC=30 m，点C与点A恰好在同一水平线上，点A、B、P、C在同一平面内．

    （1）求居民楼AB的高度；

    （2）求C、A之间的距离．（结果保留根号）

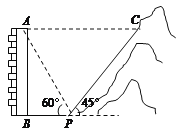
    查看答案和解析>>

    同步练习册答案