
【题目】一元二次方程x(x﹣2)=2﹣x的正整数根是 .
科目:初中数学 来源: 题型:
【题目】复习课中,教师给出关于x的函数y=﹣2mx+m﹣1(m≠0).学生们在独立思考后,给出了5条关于这个函数的结论: ①此函数是一次函数,但不可能是正比例函数;
②函数的值y 随着自变量x的增大而减小;
③该函数图象与y轴的交点在y轴的正半轴上;
④若函数图象与x轴交于A(a,0),则a<0.5;
⑤此函数图象与直线y=4x﹣3、y轴围成的面积必小于0.5.
对于以上5个结论是正确有( )个.
A.4
B.3
C.2
D.0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某跳水队为了解运动员的年龄情况,作了一次年龄调查,根据跳水运动员的年龄(单位:岁),绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:
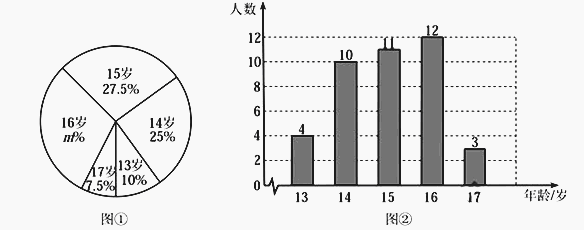
(1)本次接受调查的跳水运动员人数为 ,图①中![]() 的值为 ;
的值为 ;
(2)求统计的这组跳水运动员年龄数据的平均数、众数和中位数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用配方法解方程x2+6x﹣5=0时,此方程可变形为( )
A.(x+3)2=14
B.(x﹣3)2=14
C.(x+3)2=11
D.(x+6)2=14
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,甲、乙为两座建筑物,它们之间的水平距离BC为30m,在A点测得D点的仰角∠EAD为45°,在B点测得D点的仰角∠CBD为60°,求这两座建筑物的高度(结果保留根号)
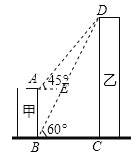
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与直线
与直线![]() 相交于
相交于![]() 两点,且抛物线经过点
两点,且抛物线经过点![]() .
.
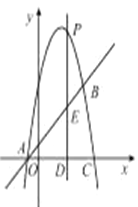
(1)求抛物线的解析式;
(2)点![]() 是抛物线上的一个动点(不与点
是抛物线上的一个动点(不与点![]() 、点
、点![]() 重合),过点
重合),过点![]() 作直线
作直线![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]() .
.
①当![]() 时,求
时,求![]() 点坐标;
点坐标;
② 是否存在点![]() 使
使![]() 为等腰三角形,若存在请直接写出点
为等腰三角形,若存在请直接写出点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一艘渔船位于港口![]() 的北偏东
的北偏东![]() 方向,距离港口
方向,距离港口![]() 海里
海里![]() 处,它沿北偏西
处,它沿北偏西![]() 方向航行至
方向航行至![]() 处突然出现故障,在
处突然出现故障,在![]() 处等待救援,
处等待救援,![]() 之间的距离为
之间的距离为![]() 海里,救援船从港口
海里,救援船从港口![]() 出发
出发![]() 分钟到达
分钟到达![]() 处,求救援的艇的航行速度.
处,求救援的艇的航行速度.![]() ,结果取整数)
,结果取整数)
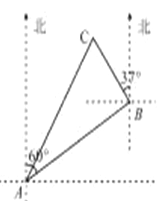
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题如图,D是BC上一点,若AB=10,AD=8,AC=17,BD=6,求BC的长.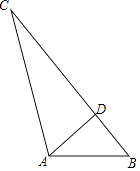
(1)已知:x= ![]() +1,y=
+1,y= ![]() ﹣1,求
﹣1,求 ![]() 的值;
的值;
(2)如图,D是BC上一点,若AB=10,AD=8,AC=17,BD=6,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某日的钱塘江观潮信息如表:

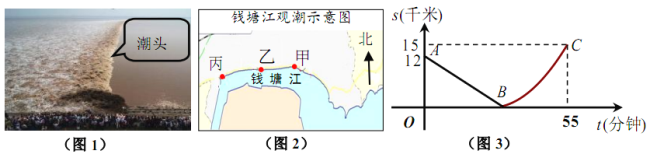
按上述信息,小红将“交叉潮”形成后潮头与乙地之间的距离![]() (千米)与时间
(千米)与时间![]() (分钟)的函数关系用图3表示,其中:“11:40时甲地‘交叉潮’的潮头离乙地12千米”记为点
(分钟)的函数关系用图3表示,其中:“11:40时甲地‘交叉潮’的潮头离乙地12千米”记为点![]() ,点
,点![]() 坐标为
坐标为![]() ,曲线
,曲线![]() 可用二次函数
可用二次函数![]() (
(![]() ,
,![]() 是常数)刻画.
是常数)刻画.
(1)求![]() 的值,并求出潮头从甲地到乙地的速度;
的值,并求出潮头从甲地到乙地的速度;
(2)11:59时,小红骑单车从乙地出发,沿江边公路以![]() 千米/分的速度往甲地方向去看潮,问她几分钟后与潮头相遇?
千米/分的速度往甲地方向去看潮,问她几分钟后与潮头相遇?
(3)相遇后,小红立即调转车头,沿江边公路按潮头速度与潮头并行,但潮头过乙地后均匀加速,而单车最高速度为![]() 千米/分,小红逐渐落后,问小红与潮头相遇到落后潮头1.8千米共需多长时间?(潮水加速阶段速度
千米/分,小红逐渐落后,问小红与潮头相遇到落后潮头1.8千米共需多长时间?(潮水加速阶段速度![]() ,
,![]() 是加速前的速度).
是加速前的速度).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com