
【题目】如图,抛物线![]() 与直线
与直线![]() 相交于
相交于![]() 两点,且抛物线经过点
两点,且抛物线经过点![]() .
.
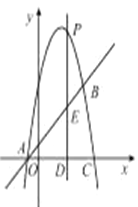
(1)求抛物线的解析式;
(2)点![]() 是抛物线上的一个动点(不与点
是抛物线上的一个动点(不与点![]() 、点
、点![]() 重合),过点
重合),过点![]() 作直线
作直线![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]() .
.
①当![]() 时,求
时,求![]() 点坐标;
点坐标;
② 是否存在点![]() 使
使![]() 为等腰三角形,若存在请直接写出点
为等腰三角形,若存在请直接写出点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
【答案】(1)y=﹣x2+4x+5;(2)①P点坐标为(2,9)或(6,﹣7);②(![]() ,
,![]() )或(4+
)或(4+![]() ,﹣4
,﹣4![]() ﹣8)或(4﹣
﹣8)或(4﹣![]() ,4
,4![]() ﹣8)或(0,5).
﹣8)或(0,5).
【解析】
试题分析:(1)由直线解析式可求得B点坐标,由A、B、C三点的坐标,利用待定系数法可求得抛物线解析式;
(2)①可设出P点坐标,则可表示出E、D的坐标,从而可表示出PE和ED的长,由条件可知到关于P点坐标的方程,则可求得P点坐标;
②由E、B、C三点坐标可表示出BE、CE和BC的长,由等腰三角形的性质可得到关于E点坐标的方程,可求得E点坐标,则可求得P点坐标.
试题解析:(1)∵点B(4,m)在直线y=x+1上,
∴m=4+1=5,
∴B(4,5),
把A、B、C三点坐标代入抛物线解析式可得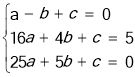 ,解得
,解得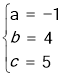 ,
,
∴抛物线解析式为y=﹣x2+4x+5;
(2)①设P(x,﹣x2+4x+5),则E(x,x+1),D(x,0),
则PE=|﹣x2+4x+5﹣(x+1)|=|﹣x2+3x+4|,DE=|x+1|,
∵PE=2ED,
∴|﹣x2+3x+4|=2|x+1|,
当﹣x2+3x+4=2(x+1)时,解得x=﹣1或x=2,但当x=﹣1时,P与A重合不合题意,舍去,
∴P(2,9);
当﹣x2+3x+4=﹣2(x+1)时,解得x=﹣1或x=6,但当x=﹣1时,P与A重合不合题意,舍去,
∴P(6,﹣7);
综上可知P点坐标为(2,9)或(6,﹣7);
②设P(x,﹣x2+4x+5),则E(x,x+1),且B(4,5),C(5,0),
∴BE=![]() |x﹣4|,CE=
|x﹣4|,CE=![]() ,BC=
,BC=![]() ,
,
当△BEC为等腰三角形时,则有BE=CE、BE=BC或CE=BC三种情况,
当BE=CE时,则![]() |x﹣4|=
|x﹣4|=![]() ,解得x=
,解得x=![]() ,此时P点坐标为(
,此时P点坐标为(![]() ,
,![]() );
);
当BE=BC时,则![]() |x﹣4|=
|x﹣4|=![]() ,解得x=4+
,解得x=4+![]() 或x=4﹣
或x=4﹣![]() ,此时P点坐标为(4+
,此时P点坐标为(4+![]() ,﹣4
,﹣4![]() ﹣8)或(4﹣
﹣8)或(4﹣![]() ,4
,4![]() ﹣8);
﹣8);
当CE=BC时,则![]() =
=![]() ,解得x=0或x=4,当x=4时E点与B点重合,不合题意,舍去,此时P点坐标为(0,5);
,解得x=0或x=4,当x=4时E点与B点重合,不合题意,舍去,此时P点坐标为(0,5);
综上可知存在满足条件的点P,其坐标为(![]() ,
,![]() )或(4+
)或(4+![]() ,﹣4
,﹣4![]() ﹣8)或(4﹣
﹣8)或(4﹣![]() ,4
,4![]() ﹣8)或(0,5).
﹣8)或(0,5).


科目:初中数学 来源: 题型:
【题目】规定:[x]表示不大于x的最大整数,(x)表示不小于x的最小整数,[x)表示最接近x的整数(x≠n+0.5,n为整数),例如:[2.3]=2,(2.3)=3,[2.3)=2.则下列说法正确的是 .(写出所有正确说法的序号)
①当x=1.7时,[x]+(x)+[x)=6;
②当x=﹣2.1时,[x]+(x)+[x)=﹣7;
③方程4[x]+3(x)+[x)=11的解为1<x<1.5;
④当﹣1<x<1时,函数y=[x]+(x)+x的图象与正比例函数y=4x的图象有两个交点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现今“微信运动”被越来越多的人关注和喜爱,某兴趣小组随机调查了我市![]() 名教师某日“微信运动”中的步数情况进行统计整理,绘制了如下的统计图表(不完整):
名教师某日“微信运动”中的步数情况进行统计整理,绘制了如下的统计图表(不完整):
步数 | 频数 | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
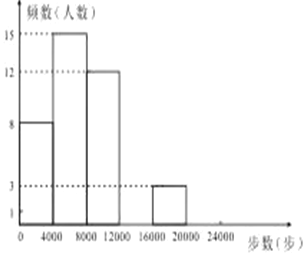
请根据以上信息,解答下列问题:
(1)写出![]() 的值并补全频数分布直方图;
的值并补全频数分布直方图;
(2)本市约有![]() 名教师,用调查的样本数据估计日行走步数超过
名教师,用调查的样本数据估计日行走步数超过![]() 步(包含
步(包含![]() 步)的教师有多少名?
步)的教师有多少名?
(3)若在![]() 名被调查的教师中,选取日行走步数超过
名被调查的教师中,选取日行走步数超过![]() 步(包含
步(包含![]() 步的两名教师与大家分享心得,求被选取的两名教师恰好都在
步的两名教师与大家分享心得,求被选取的两名教师恰好都在![]() 步(包含
步(包含![]() 步)以上的概率.
步)以上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图1在锐角△ABC中,∠ABC=45°,AD⊥BC于点D,BE⊥AC于点E,BE与AD交于点F.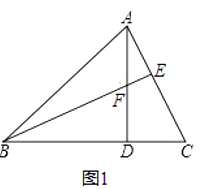
(1)若BF=5,DC=3,求AB的长;
(2)在图1上过点F作BE的垂线,过点A作AB的垂线,链条垂线交于点G,连接BG,得如图2.
①求证:∠BGF=45°;
②求证:AB=AG+ ![]() AF.
AF.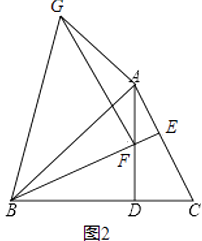
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一根弹簧长8 cm,它所挂物体的质量不能超过5 kg,并且所挂的物体每增加1 kg,弹簧就伸长0.5 cm,则挂上物体后弹簧的长度y(cm)与所挂物体的质量x(kg)(0≤x≤5)之间的关系式为( )
A. y=0.5(x+8)B. y=0.5x-8C. y=0.5(x-8)D. y=0.5x+8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com