
【题目】已知,如图1在锐角△ABC中,∠ABC=45°,AD⊥BC于点D,BE⊥AC于点E,BE与AD交于点F.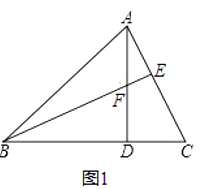
(1)若BF=5,DC=3,求AB的长;
(2)在图1上过点F作BE的垂线,过点A作AB的垂线,链条垂线交于点G,连接BG,得如图2.
①求证:∠BGF=45°;
②求证:AB=AG+ ![]() AF.
AF.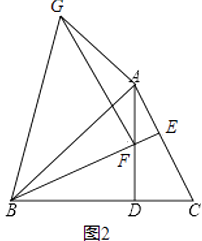
【答案】
(1)解:如图1中,
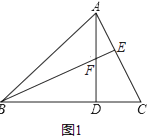
∵∠ABC=45°,AD⊥BC,
∴∠ADB=90°,△ADB是等腰直角三角形,
∴AD=BD,
∵BE⊥AC,
∴∠AEF=∠BDF=90°,
∵∠AFE=∠BFD,
∴∠EAF=∠FBD,∵∠BDF=∠ADC=90°,
∴△BDF≌△ADC,
∴DF=DC=3,
在Rt△BDF中,BD= ![]() =4,
=4,
∴AB= ![]() BD=4
BD=4 ![]()
(2)①证明:如图2中,设AB交GF于O.
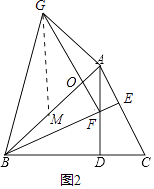
∵∠GAO=∠OFB=90°,∠AOG=∠BOF,
∴△AOG≌△FOB,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,∵∠BOG=∠AOF,
,∵∠BOG=∠AOF,
∴△BOG∽△FOA,
∴∠BGO=∠OAF=45°,
∴∠BGF=45°.
②证明:如图2中,在AB上截取AM=AG,则∠MGA=∠BGF=45°,
∴∠BCM=∠FCA,
∵BC= ![]() FG,GM=
FG,GM= ![]() AC,
AC,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴△BGM∽△FGA,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴BM= ![]() AF,
AF,
∴AB=AM+BM=AG+ ![]() AF.
AF.
【解析】①根据题意得到△ADB是等腰直角三角形,得到AD=BD,得到△BDF≌△ADC,得到DF=DC=3,根据勾股定理求出BD =4,得到AB= ![]() BD=4
BD=4 ![]() ;②在AB上截取AM=AG,则∠MGA=∠BGF=45°,得到∠BCM=∠FCA,得出△BGM∽△FGA,求出BM=
;②在AB上截取AM=AG,则∠MGA=∠BGF=45°,得到∠BCM=∠FCA,得出△BGM∽△FGA,求出BM= ![]() AF,求出AB=AM+BM=AG+
AF,求出AB=AM+BM=AG+ ![]() AF.
AF.
【考点精析】根据题目的已知条件,利用相似三角形的判定与性质的相关知识可以得到问题的答案,需要掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.


科目:初中数学 来源: 题型:
【题目】某学校初三学生进行1500米长跑体能测试,规定时间6.6分钟为达标成绩,甲、乙两名同学的成绩分别是5.8分钟和7.5分钟;以下表示两位同学成绩正确的是( )
A.甲:-0.2,乙:+0.8B.甲:+0.8,乙:+0.9
C.甲:-0.8,乙:+0.9D.甲:+0.9,乙:-0.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与直线
与直线![]() 相交于
相交于![]() 两点,且抛物线经过点
两点,且抛物线经过点![]() .
.
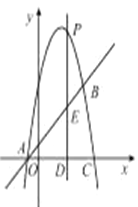
(1)求抛物线的解析式;
(2)点![]() 是抛物线上的一个动点(不与点
是抛物线上的一个动点(不与点![]() 、点
、点![]() 重合),过点
重合),过点![]() 作直线
作直线![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]() .
.
①当![]() 时,求
时,求![]() 点坐标;
点坐标;
② 是否存在点![]() 使
使![]() 为等腰三角形,若存在请直接写出点
为等腰三角形,若存在请直接写出点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题如图,D是BC上一点,若AB=10,AD=8,AC=17,BD=6,求BC的长.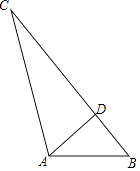
(1)已知:x= ![]() +1,y=
+1,y= ![]() ﹣1,求
﹣1,求 ![]() 的值;
的值;
(2)如图,D是BC上一点,若AB=10,AD=8,AC=17,BD=6,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给出下列定义:顺次连接任意一个四边形各边中点所得的四边形叫中点四边形,下列说法:
①如图①,四边形ABCD中,点E,F,G,H分别为边AB,BC,CD,DA的中点,则中点四边形EFGH是平行四边形.
②如图②,点P是四边形ABCD内一点,且满足PA=PB,PC=PD,∠APB=∠CPD,点E,F,G,H分别为边AB,BC,CD,DA的中点,则中点四边形EFGH是菱形
③在(2)中增加条件∠APB=∠CPD=90°,其他条件不变,则中点四边形EFGH是正方形
其中,正确的有( )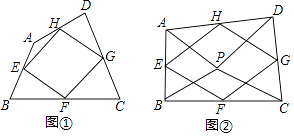
A.0个
B.1个
C.2个
D.3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在菱形ABCD中,E、F分别在BC和CD上,且△AEF是等边三角形,AE=AB,则∠BAD等于( )
A.95°
B.100°
C.105°
D.120°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】只需用两个钉子就可以把木条固定在墙上,其中蕴含的数学道理是( )
A. 线段有两个端点 B. 两点确定一条直线
C. 两点之间,线段最短 D. 线段可以比较大小
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com