
【题目】综合题如图,D是BC上一点,若AB=10,AD=8,AC=17,BD=6,求BC的长.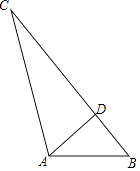
(1)已知:x= ![]() +1,y=
+1,y= ![]() ﹣1,求
﹣1,求 ![]() 的值;
的值;
(2)如图,D是BC上一点,若AB=10,AD=8,AC=17,BD=6,求BC的长.
【答案】
(1)解:∵x= ![]() +1,y=
+1,y= ![]() ﹣1,
﹣1,
∴x+y=2 ![]() ,x﹣y=2,
,x﹣y=2,
∴ ![]() =
= ![]() =
= ![]() =
= ![]()
(2)解:解:∵BD2+AD2=62+82=102=AB2,
∴△ABD是直角三角形,
∴AD⊥BC,
在Rt△ACD中,CD= ![]() =15,
=15,
∴BC=BD+CD=6+15=21,
答:BC的长是21.
【解析】①先把原分式的分子、分母分解因式,化简为最简分式;再化简出x+y=2 ![]() ,x﹣y=2,的值,代入计算即可.②根据勾股定理的逆定理得到△ABD是直角三角形,根据勾股定理求出CD =15,BC=BD+CD=6+15=21.
,x﹣y=2,的值,代入计算即可.②根据勾股定理的逆定理得到△ABD是直角三角形,根据勾股定理求出CD =15,BC=BD+CD=6+15=21.
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2,以及对勾股定理的逆定理的理解,了解如果三角形的三边长a、b、c有下面关系:a2+b2=c2,那么这个三角形是直角三角形.


科目:初中数学 来源: 题型:
【题目】将一个直角三角形纸片![]() 放置在平面直角坐标系中,点
放置在平面直角坐标系中,点![]() ,点
,点![]() ,点
,点![]() .
.![]() 是边
是边![]() 上的一点(点
上的一点(点![]() 不与点
不与点![]() 重合),沿着
重合),沿着![]() 折叠该纸片,得点
折叠该纸片,得点![]() 的对应点
的对应点![]() .
.
(1)如图①,当点![]() 在第一象限,且满足
在第一象限,且满足![]() 时,求点
时,求点![]() 的坐标;
的坐标;
(2)如图②,当![]() 为
为![]() 中点时,求
中点时,求![]() 的长;
的长;
(3)当![]() 时,求点
时,求点![]() 的坐标(直接写出结果即可).
的坐标(直接写出结果即可).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图1在锐角△ABC中,∠ABC=45°,AD⊥BC于点D,BE⊥AC于点E,BE与AD交于点F.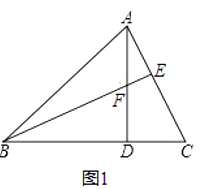
(1)若BF=5,DC=3,求AB的长;
(2)在图1上过点F作BE的垂线,过点A作AB的垂线,链条垂线交于点G,连接BG,得如图2.
①求证:∠BGF=45°;
②求证:AB=AG+ ![]() AF.
AF.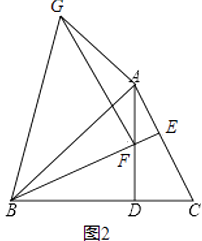
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com