
【题目】如图所示,直线l:y=3x+3与x轴交于点A,与y轴交于点B.把△AOB沿y轴翻折,点A落到点C,抛物线过点B、C和D(3,0).

(1)求直线BD和抛物线的解析式.
(2)若BD与抛物线的对称轴交于点M,点N在坐标轴上,以点N、B、D为顶点的三角形与△MCD相似,求所有满足条件的点N的坐标.
(3)在抛物线上是否存在点P,使S△PBD=6?若存在,求出点P的坐标;若不存在,说明理由.
【答案】(1)y=(x﹣1)(x﹣3)=x2﹣4x+3;(2)点N坐标为:(0,0),(﹣3,0)或(0,﹣3);(3)在抛物线上存在点P,使S△PBD=6,点P的坐标为(4,3)或(﹣1,8).
【解析】
试题分析:(1)由待定系数法求出直线BD和抛物线的解析式;
(2)首先确定△MCD为等腰直角三角形,因为△BND与△MCD相似,所以△BND也是等腰直角三角形.如答图1所示,符合条件的点N有3个;
(3)如答图2、答图3所示,解题关键是求出△PBD面积的表达式,然后根据S△PBD=6的已知条件,列出一元二次方程求解.
解:(1)∵直线l:y=3x+3与x轴交于点A,与y轴交于点B,
∴A(﹣1,0),B(0,3);
∵把△AOB沿y轴翻折,点A落到点C,∴C(1,0).
设直线BD的解析式为:y=kx+b,
∵点B(0,3),D(3,0)在直线BD上,
∴![]() ,
,
解得k=﹣1,b=3,
∴直线BD的解析式为:y=﹣x+3.
设抛物线的解析式为:y=a(x﹣1)(x﹣3),
∵点B(0,3)在抛物线上,
∴3=a×(﹣1)×(﹣3),
解得:a=1,
∴抛物线的解析式为:y=(x﹣1)(x﹣3)=x2﹣4x+3.
(2)抛物线的解析式为:y=x2﹣4x+3=(x﹣2)2﹣1,
∴抛物线的对称轴为直线x=2,顶点坐标为(2,﹣1).
直线BD:y=﹣x+3与抛物线的对称轴交于点M,令x=2,得y=1,
∴M(2,1).
设对称轴与x轴交点为点F,则CF=FD=MF=1,
∴△MCD为等腰直角三角形.
∵以点N、B、D为顶点的三角形与△MCD相似,
∴△BND为等腰直角三角形.
如答图1所示:
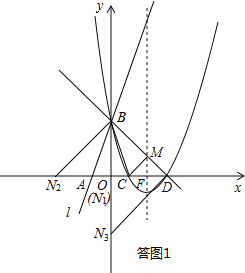
(I)若BD为斜边,则易知此时直角顶点为原点O,
∴N1(0,0);
(II)若BD为直角边,B为直角顶点,则点N在x轴负半轴上,
∵OB=OD=ON2=3,
∴N2(﹣3,0);
(III)若BD为直角边,D为直角顶点,则点N在y轴负半轴上,
∵OB=OD=ON3=3,
∴N3(0,﹣3).
∴满足条件的点N坐标为:(0,0),(﹣3,0)或(0,﹣3).
(3)假设存在点P,使S△PBD=6,设点P坐标为(m,n).
(I)当点P位于直线BD上方时,如答图2所示:
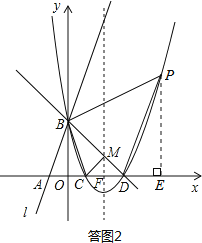
过点P作PE⊥x轴于点E,则PE=n,DE=m﹣3.
S△PBD=S梯形PEOB﹣S△BOD﹣S△PDE=![]() (3+n)m﹣
(3+n)m﹣![]() ×3×3﹣
×3×3﹣![]() (m﹣3)n=6,
(m﹣3)n=6,
化简得:m+n=7 ①,
∵P(m,n)在抛物线上,
∴n=m2﹣4m+3,
代入①式整理得:m2﹣3m﹣4=0,
解得:m1=4,m2=﹣1,
∴n1=3,n2=8,
∴P1(4,3),P2(﹣1,8);
(II)当点P位于直线BD下方时,如答图3所示:
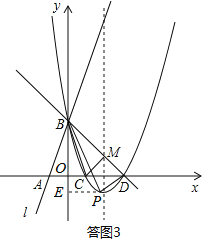
过点P作PE⊥y轴于点E,则PE=m,OE=﹣n,BE=3﹣n.
S△PBD=S梯形PEOD+S△BOD﹣S△PBE=![]() (3+m)(﹣n)+
(3+m)(﹣n)+![]() ×3×3﹣
×3×3﹣![]() (3﹣n)m=6,
(3﹣n)m=6,
化简得:m+n=﹣1 ②,
∵P(m,n)在抛物线上,
∴n=m2﹣4m+3,
代入②式整理得:m2﹣3m+4=0,△=﹣7<0,此方程无解.
故此时点P不存在.
综上所述,在抛物线上存在点P,使S△PBD=6,点P的坐标为(4,3)或(﹣1,8).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,E为BC上一点,DF⊥AE于F.

(1)△ABE与△ADF相似吗?请说明理由.
(2)若AB=6,AD=12,BE=8,求DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
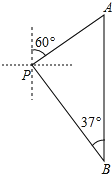
【题目】如图,小明从P处出发,沿北偏东60°方向行驶200米到达A处,接着向正南方向行驶一段时间到达B处.在B处观测到出发时所在的P处在北偏西37°方向上,这时P、B两点相距多少米?(精确到1米,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,
![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
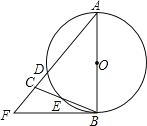
【题目】如图,在△ABC中,AB=AC=10,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且∠CBF=![]() ∠A,tan∠CBF=
∠A,tan∠CBF=![]() ,则CF的长为( )
,则CF的长为( )
A.![]() B.
B.![]()
![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)(a2)3(a2)4÷(a2)5 (2)(2x+3y)(3y-2x)-(x-3y)(y+3x)
(3)(x-2)(x+2)(x2+4) (4) 1232-122×124;
(5)(a+b-1)2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,OC是∠AOD的平分线,OE是∠BOD的平分线.
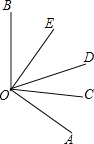
(1)若∠AOB=120°,则∠COE是多少度?
(2)若∠EOC=65°,∠DOC=25°,则∠BOE是多少度?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com