
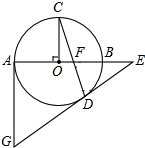
 如图,AB是⊙O直径,OC⊥AB,弦CD与OB交于点F,过点D、A分别作⊙O的切线交于点G,切线GD与AB延长线交于点E.
如图,AB是⊙O直径,OC⊥AB,弦CD与OB交于点F,过点D、A分别作⊙O的切线交于点G,切线GD与AB延长线交于点E.| 1 |
| 2 |
 (1)证明:连接OD,
(1)证明:连接OD,| OD |
| AG |
| DE |
| AE |
| OE |
| GE |
| 3 |
| 6 |
| x |
| AE |
| OE |
| 6+x |
| 1 |
| 2 |
| 1 |
| 2 |


科目:初中数学 来源: 题型:
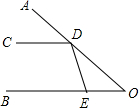 如图所示,∠AOB的两边OA,OB均为平面反光镜,∠AOB=30°,在OB上有一点E,从E点射出一束光线经OA上的点D反射后,反射光线DC恰好与OB平行.
如图所示,∠AOB的两边OA,OB均为平面反光镜,∠AOB=30°,在OB上有一点E,从E点射出一束光线经OA上的点D反射后,反射光线DC恰好与OB平行.查看答案和解析>>
科目:初中数学 来源: 题型:
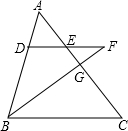 已知如图,D是△ABC的边AB上一点,DE∥BC,交边AC于点E,延长DE至点F,使EF=DE,联结BF,交边AC于点G,联结CF
已知如图,D是△ABC的边AB上一点,DE∥BC,交边AC于点E,延长DE至点F,使EF=DE,联结BF,交边AC于点G,联结CF| AE |
| AC |
| EG |
| CG |
查看答案和解析>>
科目:初中数学 来源: 题型:
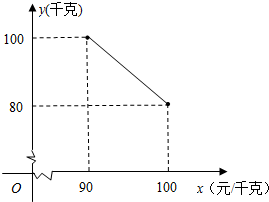 某茶叶专卖店经销一种崂山绿茶,每千克成本80元.据销售人员调查发现,每月的销售量y(千克)与销售单价x(元/千克)之间存在如图所示的变化规律.
某茶叶专卖店经销一种崂山绿茶,每千克成本80元.据销售人员调查发现,每月的销售量y(千克)与销售单价x(元/千克)之间存在如图所示的变化规律.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
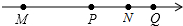 如图,四个有理数在数轴上的对应点M,P,N,Q,若点M,N表示的有理数互为相反数,则图中表示绝对值最小的数的点是( )
如图,四个有理数在数轴上的对应点M,P,N,Q,若点M,N表示的有理数互为相反数,则图中表示绝对值最小的数的点是( )| A、点M | B、点N | C、点P | D、点Q |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com