
【题目】已知![]() 是一段圆弧上的两点,且在直线
是一段圆弧上的两点,且在直线![]() 的同侧,分别过这两点作
的同侧,分别过这两点作![]() 的垂线,垂足为
的垂线,垂足为
![]() 是
是![]() 上一动点,连接
上一动点,连接![]() ,且
,且![]() .
.
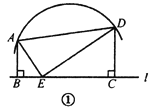
(1)如图①,如果![]() ,且
,且![]() ,求
,求![]() 的长;
的长;
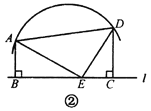
(2)如图②,若点![]() 恰为这段圆弧的圆心,则线段
恰为这段圆弧的圆心,则线段![]() 之间有怎样的等量关系?请写出你的结论并予以证明.再探究:当
之间有怎样的等量关系?请写出你的结论并予以证明.再探究:当![]() 分别在直线
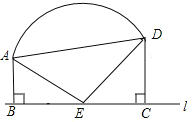
分别在直线![]() 两侧且
两侧且![]() ,而其余条件
,而其余条件
不变时,线段![]() 之间又有怎样的等量关系?请直接写出结论,不必证明.
之间又有怎样的等量关系?请直接写出结论,不必证明.
【答案】(1) 2![]() ;(2) (i)猜想:AB+CD=BC; (ii)当A,D分别在直线l两侧时,有如下等量关系:AB-CD=BC(AB>CD)或CD-AB=BC(AB<CD).
;(2) (i)猜想:AB+CD=BC; (ii)当A,D分别在直线l两侧时,有如下等量关系:AB-CD=BC(AB>CD)或CD-AB=BC(AB<CD).
【解析】分析:(1)根据两角对应相等证明Rt△ABE∽Rt△ECD,然后根据相似三角形的对应边的比相等求得CD的长,再运用勾股定理就可计算出AD的长;
(2)可以证明Rt△ABE≌Rt△ECD,得到对应线段相等,根据图形就可得到线段之间的和差关系.
详解:(1)∵AB⊥l于B,DC⊥l于C,
∴∠ABE=∠ECD=90°.
∵∠BEA+∠AED+∠CED=180°,且∠AED=90°,
∴∠CED=90°-∠BEA.
又∵∠BAE=90°-∠BEA,
∴∠BAE=∠CED.
∴Rt△ABE∽Rt△ECD.
∴![]() .
.
∵BE:EC=1:3 BC=16,
∴BE=4,EC=12.
又∵AB=6,
∴CD=![]() =
=![]() =8.
=8.
在Rt△AED中,由勾股定理得
AD=![]() =2
=2![]() .
.
(2)(i)猜想:AB+CD=BC.
证明:在Rt△ABE中,∵∠ABE=90°
∴∠BAE=90°-∠AEB,
又∵∠AEB+∠AED+∠CED=180°,且∠AED=90°,
∴∠CED=90°-∠AEB.
∴∠BAE=∠CED.
∵DC⊥BC于点C,
∴∠ECD=90°.
由已知,有AE=ED,
在Rt△ABE和Rt△ECD中,
∠ABE=∠ECD=90°,∠BAE=∠CED,AE=ED,,
∴Rt△ABE≌Rt△ECD(AAS).
∴AB=EC,BE=CD.
∴BC=BE+EC=CD+AB,即AB+CD=BC.
(ii)当A,D分别在直线l两侧时,线段AB,BC,CD有如下等量关系:
AB-CD=BC(AB>CD)或CD-AB=BC(AB<CD).


 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:初中数学 来源: 题型:
【题目】已知一次函数图像过点P(0,6),且平行于直线y=-2x
(1)求该一次函数的解析式
(2)若点A(![]() ,a)、B(2,b)在该函数图像上,试判断a、b的大小关系,并说明理由。
,a)、B(2,b)在该函数图像上,试判断a、b的大小关系,并说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了开阔学生的视野,积极组织学生参加课外读书活动.“放飞梦想”读书小组协助老师随机抽取本校的部分学生,调查他们最喜爱的图书类别(图书分为文学类、艺体类、科普类、其他等四类),并将调查结果绘制成如下两幅不完整的统计图,请你结合图中的信息解答下列问题:
(1)求被调查的学生人数;
(2)补全条形统计图;
(3)已知该校有1200名学生,估计全校最喜爱文学类图书的学生有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小强与小刚都住在安康小区,在同一所学校读书.某天早上,小强![]() 从安康小区站乘坐校车去学校,途中需停靠两个站点才能到达学校站点,且每个站点停留
从安康小区站乘坐校车去学校,途中需停靠两个站点才能到达学校站点,且每个站点停留![]() 分钟,校车行驶途中始终保持匀速.当天早上,小刚
分钟,校车行驶途中始终保持匀速.当天早上,小刚![]() 从安康小区站乘坐出租车沿相同路线出发,出租车匀速行驶,比小强乘坐的校车早
从安康小区站乘坐出租车沿相同路线出发,出租车匀速行驶,比小强乘坐的校车早![]() 分钟到学校站点.他们乘坐的车辆从安康小区站出发所行驶路程
分钟到学校站点.他们乘坐的车辆从安康小区站出发所行驶路程![]() (千米)与行驶时间
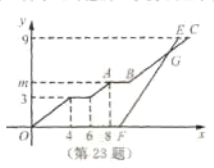
(千米)与行驶时间![]() (分钟)之间的函数图象如图所示.
(分钟)之间的函数图象如图所示.
(1)求点![]() 的纵坐标
的纵坐标![]() 的值;
的值;
(2)小刚乘坐出租车出发后经过多少分钟追到小强所乘坐的校车?并求此时他们距学校站点的路程.
查看答案和解析>>
科目:初中数学 来源: 题型:
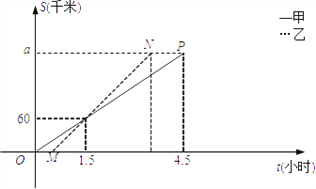
【题目】甲、乙两车从A地将一批物品匀速运往B地,已知甲出发0.5h后乙开始出发,如图,线段OP、MN分别表示甲、乙两车离A地的距离S(km)与时间t(h)的关系,请结合图中的信息解决如下问题:
(1)计算甲、乙两车的速度及a的值;
(2)乙车到达B地后以原速立即返回.
①在图中画出乙车在返回过程中离A地的距离S(km)与时间t(h)的函数图象;②请问甲车在离B地多远处与返程中的乙车相遇?
查看答案和解析>>
科目:初中数学 来源: 题型:
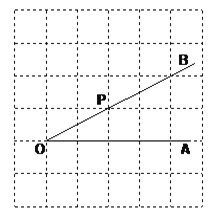
【题目】如图,点P是![]() 的边OB上的一点。
的边OB上的一点。
过点P画OA的垂线,垂足为H;
过点P画OB的垂线,交OA于点C;
线段PH的长度是点P到 的距离,_____ 是点C到直线OB的距离。因为直线外一点到直线上各点连接的所有线段中,垂线段最短,所以线段PC、PH、OC这三条线段大小关系是 。(用“<”号连接)
查看答案和解析>>
科目:初中数学 来源: 题型:
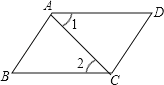
【题目】 根据题意,完成推理填空:如图,AB∥CD,∠1=∠2,试说明∠B=∠D.
解:∵∠1=∠2(已知)
∴ (內错角相等,两直线平行)
∴∠BAD+∠B=180°(两直线平行,同旁内角互补)
∵AB∥CD
∴ + =180°,
∴∠B=∠D
查看答案和解析>>
科目:初中数学 来源: 题型:
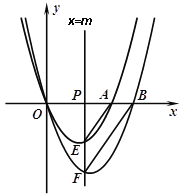
【题目】如图,动直线![]() (
(![]() )分别交x轴,抛物线
)分别交x轴,抛物线![]() 和
和![]() 于点P,E,F,设点A,B为抛物线
于点P,E,F,设点A,B为抛物线![]() ,
, ![]() 与x轴的一个交点,连结AE,BF.
与x轴的一个交点,连结AE,BF.
(1)求点A,B的坐标.
(2)当![]() 时,判断直线AE与BF的位置关系,并说明理由.
时,判断直线AE与BF的位置关系,并说明理由.
(3)连结BE,当![]() 时,求△BEF的面积.
时,求△BEF的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com