
【题目】已知一次函数图像过点P(0,6),且平行于直线y=-2x
(1)求该一次函数的解析式
(2)若点A(![]() ,a)、B(2,b)在该函数图像上,试判断a、b的大小关系,并说明理由。
,a)、B(2,b)在该函数图像上,试判断a、b的大小关系,并说明理由。
【答案】(1)y=-2x+6 (2)答案见解析
【解析】
(1)根据两一次函数图像平行,可得到k的值相等,因此设一次函数解析式为y=-2x+b,再将点P的坐标代入函数解析式就可求出b的值,就可得到函数解析式;
(2)利用一次函数的性质:k<0时,y随x的增大而减小,比较点A,B的横坐标的大小,就可求得a,b的大小关系
(1)解:∵ 一次函数图像过点P(0,6),且平行于直线y=-2x,
∴设这个一次函数解析式为y=-2x+b
∴b=6
∴该一次函数解析式为y=-2x+6;
(2)解:∵一次函数解析式为y=-2x+6,k=-2<0
∴y随x的增大而减小;
∵ 点A(![]() ,a)、B(2,b)在该函数图像上且
,a)、B(2,b)在该函数图像上且![]() ,
,
∴a>b


科目:初中数学 来源: 题型:
【题目】为进一步丰富学生课余文化生活和营造朝气蓬勃的校园文化氛围,学校组织学生开展了各种文体活动、社团活动,现在开展的社团活动有音乐,体育,美术,摄影四类,每个同学必须且只能从中选择参加一个社团,为了解学生参与社团活动的情况,学生会成员随机调查了一部分学生所参加的社团类别并绘制了以下两幅不完整的统计图,请你根据统计图提供的信息,解答下列问题:
社团活动条形统计图 社团活动扇形统计图


(1)本次一共调查了_____________________名同学;
(2)补全统计图;在扇形统计图中,“美术”所在扇形的圆心角的度数为_______________;
(3)小明和小亮都想报美术,摄影,体育社团,用画树状图或列表的方法,求他们恰好参加同一社团的概率。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在解决数学问题的过程中,我们常用到“分类讨论”的数学思想,下面是运用分类讨论的数学思想解决问题的过程,请仔细阅读,并解答题目后提出的探究问题.
(提出问题)三个有理数a,b,c,满足abc>0,求![]() 的值.
的值.
(解决问题)
解:由题意得:a,b,c三个有理数都为正数或其中一个为正数,另两个为负数.
①当a,b,c,都是整数,即a>0,b>0,c>0时,则![]() =
= ![]() =1+1+1=3;
=1+1+1=3;
②当a,b,c有一个为正数,另两个位负数时,设a>0,b<0,c<0,则![]() =
= ![]() =111=1;
=111=1;
所以![]() 的值为3或1.
的值为3或1.
(探究)请根据上面的解题思路解答下面的问题:
(1)三个有理数a,b,c满足abc<0,求![]() 的值;
的值;
(2)已知![]() =9,
=9,![]() =4,且a<b,求a2b的值.
=4,且a<b,求a2b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学的趣味无处不在,在学习数学的过程中,小明发现了有规律的等式:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
……
(1)从计算过程中找出规律,可知:
①![]() ;
;
② =![]() .
.
(2)计算:![]() (结果用含n的式子表示)
(结果用含n的式子表示)
(3)对于算式:![]()
①计算出算式的值(结果用乘方表示);
②直接写出结果的个位数字是几?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们规定:平面内点A到图形G上各个点的距离的最小值称为该点到这个图形的最小距离d,点A到图形G上各个点的距离的最大值称为该点到这个图形的最大距离D,定义点A到图形G的距离跨度为R=D-d.
(1)①如图1,在平面直角坐标系xOy中,图形G1为以O为圆心,2为半径的圆,直接写出以下各点到图形G1的距离跨度:
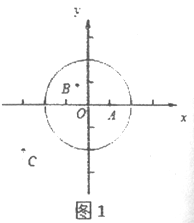
A(1,0)的距离跨度______________;
B(-![]() ,
, ![]() )的距离跨度____________;
)的距离跨度____________;
C(-3,-2)的距离跨度____________;
②根据①中的结果,猜想到图形G1的距离跨度为2的所有的点组成的图形的形状是______________.
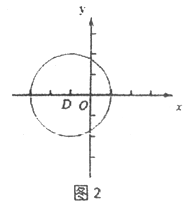
(2)如图2,在平面直角坐标系xOy中,图形G2为以D(-1,0)为圆心,2为半径的圆,直线y=k(x-1)上存在到G2的距离跨度为2的点,求k的取值范围.
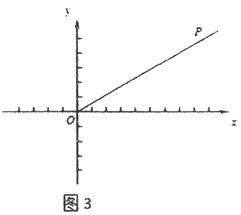
(3)如图3,在平面直角坐标系xOy中,射线OP:y=![]() x(x≥0),⊙E是以3为半径的圆,且圆心E在x轴上运动,若射线OP上存在点到⊙E的距离跨度为2,求出圆心E的横坐标xE的取值范围.
x(x≥0),⊙E是以3为半径的圆,且圆心E在x轴上运动,若射线OP上存在点到⊙E的距离跨度为2,求出圆心E的横坐标xE的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】经过建设者三年多艰苦努力地施工,贯通我市A、B两地又一条高速公路全线通车.已知原来A地到B地普通公路长150km,高速公路路程缩短了30km,如果一辆小车从A地到B地走高速公路的平均速度可以提高到原来的1.5倍,需要的时间可以比原来少用1小时.求小车走普通公路的平均速度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
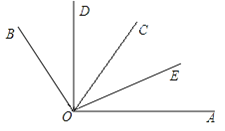
【题目】已知:如图所示,OD平分∠BOC,OE平分∠AOC.若∠BOC=70°,∠AOC=50°.
(1)求出∠AOB及其补角的度数;
(2)求出∠DOC和∠AOE的度数,并判断∠DOE 与∠AOB是否互补,并说明理由;
(3)若∠BOC=α,∠AOC=β,则∠DOE 与∠AOB是否互补,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a-b|.

利用数形结合思想回答下列问题:
①数轴上表示1和3两点之间的距离是
②数轴上表示x和-1的两点之间的距离表示为
③若x表示一个有理数,且-4<x<2,则|x-2|+|x+4|=
④若x表示一个有理数,且|x-2|+|x+4|=8,则有理数x的值是
查看答案和解析>>
科目:初中数学 来源: 题型:
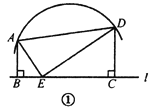
【题目】已知![]() 是一段圆弧上的两点,且在直线
是一段圆弧上的两点,且在直线![]() 的同侧,分别过这两点作
的同侧,分别过这两点作![]() 的垂线,垂足为
的垂线,垂足为
![]() 是
是![]() 上一动点,连接
上一动点,连接![]() ,且
,且![]() .
.
(1)如图①,如果![]() ,且
,且![]() ,求
,求![]() 的长;
的长;
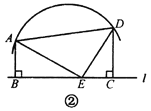
(2)如图②,若点![]() 恰为这段圆弧的圆心,则线段
恰为这段圆弧的圆心,则线段![]() 之间有怎样的等量关系?请写出你的结论并予以证明.再探究:当
之间有怎样的等量关系?请写出你的结论并予以证明.再探究:当![]() 分别在直线
分别在直线![]() 两侧且
两侧且![]() ,而其余条件
,而其余条件
不变时,线段![]() 之间又有怎样的等量关系?请直接写出结论,不必证明.
之间又有怎样的等量关系?请直接写出结论,不必证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com