
【题目】我们规定:平面内点A到图形G上各个点的距离的最小值称为该点到这个图形的最小距离d,点A到图形G上各个点的距离的最大值称为该点到这个图形的最大距离D,定义点A到图形G的距离跨度为R=D-d.
(1)①如图1,在平面直角坐标系xOy中,图形G1为以O为圆心,2为半径的圆,直接写出以下各点到图形G1的距离跨度:
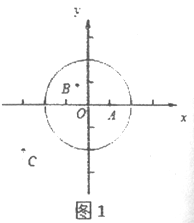
A(1,0)的距离跨度______________;
B(-![]() ,
, ![]() )的距离跨度____________;
)的距离跨度____________;
C(-3,-2)的距离跨度____________;
②根据①中的结果,猜想到图形G1的距离跨度为2的所有的点组成的图形的形状是______________.
(2)如图2,在平面直角坐标系xOy中,图形G2为以D(-1,0)为圆心,2为半径的圆,直线y=k(x-1)上存在到G2的距离跨度为2的点,求k的取值范围.
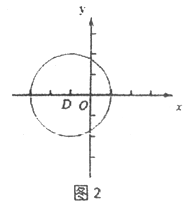
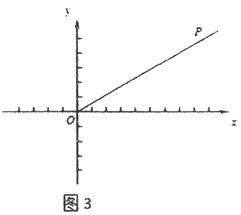
(3)如图3,在平面直角坐标系xOy中,射线OP:y=![]() x(x≥0),⊙E是以3为半径的圆,且圆心E在x轴上运动,若射线OP上存在点到⊙E的距离跨度为2,求出圆心E的横坐标xE的取值范围.
x(x≥0),⊙E是以3为半径的圆,且圆心E在x轴上运动,若射线OP上存在点到⊙E的距离跨度为2,求出圆心E的横坐标xE的取值范围.
【答案】(1)①2;2,4;②以O为圆心,半径为1的圆;(2)-![]() ≤k≤
≤k≤![]() ;(3)-1≤xE≤2 .
;(3)-1≤xE≤2 .
【解析】试题分析:(1)①先根据跨度的定义先确定出点到圆的最小距离d和最大距离D,即可得出跨度;
②分点在圆内和圆外两种情况同①的方法计算,判定得出结论;
(2)先判断出存在的点P必在圆O内,设出点P的坐标,利用点P到圆心O的距离的2倍是点P到圆的距离跨度,建立方程,由于存在距离跨度是2的点,此方程有解即可得出k的范围.
(3)同(2)方法判断出存在的点P在圆C内部,由于在射线OA上存在距离跨度是2的点,同(2)的方法建立方程,用一元二次方程根与系数的关系和根的判别式即可确定出范围.
试题解析:
(1)①∵图形G1为以O为圆心,2为半径的圆,
∴直径为4,
∵A(1,0),OA=1,
∴点A到⊙O的最小距离d=1,
点A到⊙O的最大距离D=3,
∴点A到图形G1的距离跨度R=D-d=3-1=2;
∵B![]()
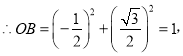
∴点B到⊙O的最小距离d=BG=OG-OB=1,
点B到⊙O的最大距离D=BF=FO+OB=2+1=3,
∴点B到图形G1的距离跨度R=D-d=3-1=2;
∵C(-3,-2),
∴OC=![]()
∴点C到⊙O的最小距离d=CD=OC-OD=![]() -2.
-2.
点C到⊙O的最大距离D=CE=OC+OE=2+![]()
∴点C到图形G1的距离跨度R=D-d=2+![]() -(
-(![]() -2))=4;
-2))=4;
故答案为2,2,4.
②a、设⊙O内一点P的坐标为(x,y),
∴OP=![]()
∴点P到⊙O的最小距离d=2-OP,点P到⊙O的最大距离D=2+OP,
∴点P到图形G1的距离跨度R=D-d=2+OP-(2-OP)=2OP;
∵图形G1的距离跨度为2,
∴2OP=2,
∴OP=1,
∴![]() =1
=1
∴x2+y2=1,
即:到图形G1的距离跨度为2的所有的点组成的图形的形状是以点O为圆心,1为半径的圆.
b、设⊙O外一点Q的坐标为(x,y),
∴OQ=![]()
∴点Q到⊙O的最小距离d=OQ-2,点P到⊙O的最大距离D=OQ+2,
∴点P到图形G1的距离跨度R=D-d=OQ+2-(OQ-2)=4;
∵图形G1的距离跨度为2,
∴此种情况不存在,
所以,到图形G1的距离跨度为2的所有的点组成的图形的形状是以点O为圆心,1为半径的圆.
故答案为:圆;
(2)设直线y=k(x+1)上存在到G2的距离跨度为2的点P(m,k(m+1)),
∴OP=![]()
由(1)②知,圆内一点到图形圆的跨度是此点到圆心距离的2倍,圆外一点到图形圆的跨度是此圆的直径,
∵图形G2为以C(1,0)为圆心,2为半径的圆,到G2的距离跨度为2的点,
∴距离跨度小于图形G2的圆的直径4,
∴点P在图形G2⊙C内部,
∴R=2OP=2![]()
∵直线y=k(x+1)上存在到G2的距离跨度为2的点P,
∴2![]() =2
=2
∴(k2+1)m2+2(k2-1)m+k2=0①,
∵存在点P,
∴方程①有实数根,
∴△=4(k2-1)2-4×(k2+1)k2=-12k2+4≥0,
![]()
(3)如图,作EC⊥OP于C,交⊙E于D、H.
由题意:⊙E是以3为半径的圆,且圆心E在x轴上运动,若射线OP上存在点到⊙E的距离跨度为2,此时以E为圆心1为半径的圆与射线OP相切,当以E为圆心1为半径的圆与射线OP有交点时,满足条件,
∴CD=2,CH=4,CE=1,
∵射线OP的解析式为y=![]() ,
,
∴∠COE=30°,OE=2CE=2,
当E′(-1,0)时,点O到⊙E的距离跨度为2,
观察图象可知,满足条件的圆心E的横坐标xE的取值范围:-1≤xE≤2.
故答案为:-1≤xE≤2.


科目:初中数学 来源: 题型:
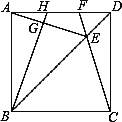
【题目】如图,在正方形ABCD中,E是对角线BD上一点,且满足BE=BC.连接CE并延长交AD于点F,连接AE,过B点作BG⊥AE于点G,延长BG交AD于点H.在下列结论中:
①AH=DF; ②∠AEF=45°; ③S四边形EFHG=S△DEF+S△AGH,
其中正确的结论有_____________________.(填正确的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1在正方形ABCD的外侧作两个等边三角形ADE和DCF,连接AF,BE.
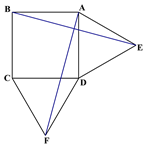
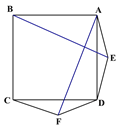

(图1) (图2) (备用图)
(1)请判断:AF与BE的数量关系是_____________,位置关系______________;
(2)如图2,若将条件“两个等边三角形ADE和DCF”变为“两个等腰三角形ADE和DCF,且EA=ED=FD=FC”,第(1)问中的结论是否仍然成立?请作出判断并给予证明;
(3)若三角形ADE和DCF为一般三角形,且AE=DF,ED=FC,第(1)问中的结论都能成立吗?请直接写出你的判断.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若八个数据x1, x2, x3, ……x8, 的平均数为8,方差为1,增加一个数据8后所得的九个数据x1, x2, x3, …x8;8的平均数![]() ________8,方差为S2 ________1.(填“>”、“=”、“<”)
________8,方差为S2 ________1.(填“>”、“=”、“<”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数图像过点P(0,6),且平行于直线y=-2x
(1)求该一次函数的解析式
(2)若点A(![]() ,a)、B(2,b)在该函数图像上,试判断a、b的大小关系,并说明理由。
,a)、B(2,b)在该函数图像上,试判断a、b的大小关系,并说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
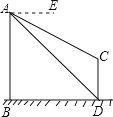
【题目】如图,AB、CD为两个建筑物,建筑物AB的高度为60米,从建筑物AB的顶点A点测得建筑物CD的顶点C点的俯角∠EAC为30°,测得建筑物CD的底部D点的俯角∠EAD为45°.
(1)求两建筑物底部之间水平距离BD的长度;
(2)求建筑物CD的高度(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
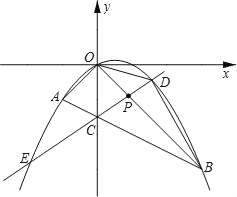
【题目】如图,在平面直角坐标系中,点A的坐标为(m,m),点B的坐标为(n,﹣n),抛物线经过A、O、B三点,连接OA、OB、AB,线段AB交y轴于点C.已知实数m、n(m<n)分别是方程x2﹣2x﹣3=0的两根.
(1)求抛物线的解析式;
(2)若点P为线段OB上的一个动点(不与点O、B重合),直线PC与抛物线交于D、E两点(点D在y轴右侧),连接OD、BD.
①当△OPC为等腰三角形时,求点P的坐标;
②求△BOD 面积的最大值,并写出此时点D的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com