
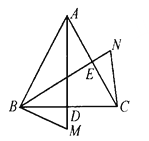
【题目】如图,AD、BE分别是等边△ABC中BC、AC上的高.M、N分别在AD、BE的延长线上,∠CBM=∠ACN.求证:AM=BN.
【答案】见解析
【解析】
根据等边三角形的性质可得∠ABC=∠ACB=60°,AB=BC,然后求出∠ABM=∠BCN,再根据等边三角形三线合一的性质求出∠BAM=∠CBN=30°,然后利用“角边角”证明△ABM和△BCN全等,再根据全等三角形对应边相等证明即可.
:∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°,AB=BC,
∵∠CBM=∠ACN,
∴∠ABC+∠CBM=∠ACB+∠ACN,
即∠ABM=∠BCN,
∵AD、BE分别是边BC、AC上的高,
∴∠BAM=∠CBN=30°,
在△ABM和△BCN中,
∠ABM=∠BCN AB=BC ∠BAM=∠CBN,
∴△ABM≌△BCN(ASA),
∴AM=BN.


科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴交于点A,与
轴交于点A,与![]() 轴交于点B,抛物线
轴交于点B,抛物线![]() 经过原点和点C(4,0),顶点D在直线AB上。
经过原点和点C(4,0),顶点D在直线AB上。
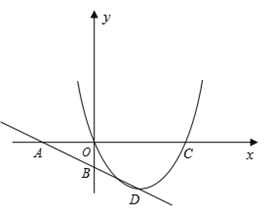
(1)求这个抛物线的解析式;
(2)在抛物线的对称轴上是否存在点P,使得以P、C、D为顶点的三角形与△ACD相似。若存在,请求出点P的坐标;若不存在,请说明理由;
(3)点Q是![]() 轴上方的抛物线上的一个动点,若
轴上方的抛物线上的一个动点,若![]() ,⊙M经过点O,C,Q,求过C点且与⊙M相切的直线解析式
,⊙M经过点O,C,Q,求过C点且与⊙M相切的直线解析式
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
问题情境
如图,同学们用矩形纸片ABCD开展数学探究活动,其中AD=8,CD=6。
操作计算
(1)如图(1),分别沿BE,DF剪去RtΔABE和RtΔCDF两张纸片,如果剩余的纸片BEDF菱形,求AE的长;

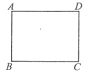
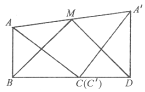
图(1) 图(2) 图(3)
操作探究
把矩形纸片ABCD沿对角线AC剪开,得到ΔABC和![]() 两张纸片
两张纸片
(2)将两张纸片如图(2)摆放,点C和![]() 重合,点B,C,D在同一条直线上,连接
重合,点B,C,D在同一条直线上,连接![]() ,记
,记![]() 的中点为M,连接BM,MD,发现ΔBMD是等腰三角形,请证明:
的中点为M,连接BM,MD,发现ΔBMD是等腰三角形,请证明:
(3)如图(3),将两张纸片叠合在一起,然后将![]() 纸片绕点B顺时针旋转a(00<a<900),连接
纸片绕点B顺时针旋转a(00<a<900),连接![]() 和
和![]() ,探究并直接写出线段
,探究并直接写出线段![]() 与
与![]() 的关系。
的关系。
查看答案和解析>>
科目:初中数学 来源: 题型:
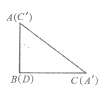
【题目】五一小长假,李军与张明相约去宁波旅游,李军从温岭北上沿海高速,同时张明从玉环芦浦上沿海高速,温岭北与玉环芦浦相距44千米,两人约好在三门服务区集合,李军由于离三门近,行驶了1.2小时先到达三门服务站等候张明,张明走了1.4小时到达三门服务站。在整个过程中,两人均保持各自的速度匀速行驶,两人相距的路程y千米与张明行驶的时间x小时的关系如图所示,下列说法错误的是( )
A.李军的速度是80千米/小时
B.张明的速度是100千米/小时
C.玉环芦浦至三门服务站的路程是140千米
D.温岭北至三门服务站的路程是44千米
查看答案和解析>>
科目:初中数学 来源: 题型:
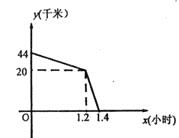
【题目】如图,在矩形ABCD中,对角线AC、BD交于点O,BE平分∠ABC交AC于点F,交AD于点E,且∠DBF=15°,求证:(1)AO=AE; (2)∠FEO的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在解决数学问题的过程中,我们常用到“分类讨论”的数学思想,下面是运用分类讨论的数学思想解决问题的过程,请仔细阅读,并解答题目后提出的探究问题.
(提出问题)三个有理数a,b,c,满足abc>0,求![]() 的值.
的值.
(解决问题)
解:由题意得:a,b,c三个有理数都为正数或其中一个为正数,另两个为负数.
①当a,b,c,都是整数,即a>0,b>0,c>0时,则![]() =
= ![]() =1+1+1=3;
=1+1+1=3;
②当a,b,c有一个为正数,另两个位负数时,设a>0,b<0,c<0,则![]() =
= ![]() =111=1;
=111=1;
所以![]() 的值为3或1.
的值为3或1.
(探究)请根据上面的解题思路解答下面的问题:
(1)三个有理数a,b,c满足abc<0,求![]() 的值;
的值;
(2)已知![]() =9,
=9,![]() =4,且a<b,求a2b的值.
=4,且a<b,求a2b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
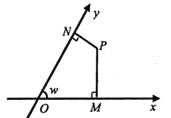
【题目】定义:在同一平面内画两条相交、有公共原点的数轴x轴和y轴,交角a≠90°,这样就在平面上建立了一个斜角坐标系,其中w叫做坐标角,对于坐标平面内任意一点P,过P作y轴和x轴的平行线,与x轴、y轴相交的点的坐标分别是a和b,则称点P的斜角坐标为(a,b).如图,w=60°,点P的斜角坐标是(1,2),过点P作x轴和y轴的垂线,垂足分别为M、N,则四边形OMPN的面积是( )
A.![]() B.
B.![]() C.
C.![]() D.3
D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们规定:平面内点A到图形G上各个点的距离的最小值称为该点到这个图形的最小距离d,点A到图形G上各个点的距离的最大值称为该点到这个图形的最大距离D,定义点A到图形G的距离跨度为R=D-d.
(1)①如图1,在平面直角坐标系xOy中,图形G1为以O为圆心,2为半径的圆,直接写出以下各点到图形G1的距离跨度:
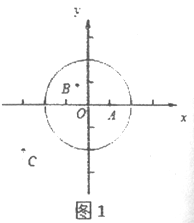
A(1,0)的距离跨度______________;
B(-![]() ,
, ![]() )的距离跨度____________;
)的距离跨度____________;
C(-3,-2)的距离跨度____________;
②根据①中的结果,猜想到图形G1的距离跨度为2的所有的点组成的图形的形状是______________.
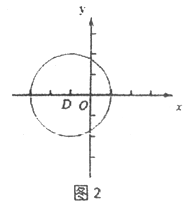
(2)如图2,在平面直角坐标系xOy中,图形G2为以D(-1,0)为圆心,2为半径的圆,直线y=k(x-1)上存在到G2的距离跨度为2的点,求k的取值范围.
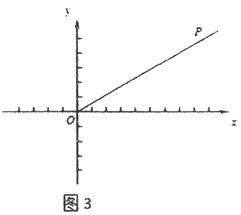
(3)如图3,在平面直角坐标系xOy中,射线OP:y=![]() x(x≥0),⊙E是以3为半径的圆,且圆心E在x轴上运动,若射线OP上存在点到⊙E的距离跨度为2,求出圆心E的横坐标xE的取值范围.
x(x≥0),⊙E是以3为半径的圆,且圆心E在x轴上运动,若射线OP上存在点到⊙E的距离跨度为2,求出圆心E的横坐标xE的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=10,点C,D在线段AB上且AC=DB=2;P是线段CD上的动点,分别以AP,PB为边在线段AB的同侧作等边△AEP和等边△PFB,连接EF,设EF的中点为G;当点P从点C运动到点D时,则点G移动路径的长是( ).
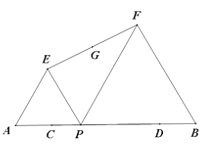
A.6B.5C.4D.3.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com