
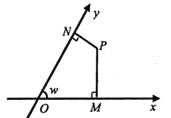
【题目】定义:在同一平面内画两条相交、有公共原点的数轴x轴和y轴,交角a≠90°,这样就在平面上建立了一个斜角坐标系,其中w叫做坐标角,对于坐标平面内任意一点P,过P作y轴和x轴的平行线,与x轴、y轴相交的点的坐标分别是a和b,则称点P的斜角坐标为(a,b).如图,w=60°,点P的斜角坐标是(1,2),过点P作x轴和y轴的垂线,垂足分别为M、N,则四边形OMPN的面积是( )
A.![]() B.
B.![]() C.
C.![]() D.3
D.3
【答案】B
【解析】
添加辅助线,将四边形OMPN转化为直角三角形和平行四边形,因此过点P作PA∥y轴,交x轴于点A,过点P作PB∥x轴交y轴于点B,易证四边形OAPB是平行四边形,利用平行四边形的性质,可知OB=PA,OA=PB,由点P的斜角坐标就可求出PB、PA的长,再利用解直角三角形分别求出PN,NB,PM,AM的长,然后根据S四边形OMPN=S△PAM+S△PBN+S平行四边形OAPB , 利用三角形的面积公式和平行四边形的面积公式,就可求出结果.
解:过点P作PA∥y轴,交x轴于点A,过点P作PB∥x轴交y轴于点B,
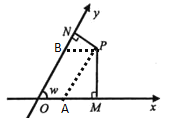
∴四边形OAPB是平行四边形,∠NBP=w=∠PAM=60°,
∴OB=PA,OA=PB
∵点P的斜角坐标为(1,2),
∴OA=1,OB=2,
∴PB=1,PA=2,
∵PM⊥x轴,PN⊥y轴,
∴∠PMA=∠PNB=90°,
在Rt△PAM中,∠PAM=60°,则∠APM=30°,
∴PA=2AM=2,即AM=1
PM=PAsin60°
∴PM=![]()
∴S△PAM=![]()
在Rt△PBN中,∠PBN=60°,则∠BPN=30°,
∴PB=2BN=1,即BN=![]()
PN=PBsin60°
∴PN=![]()
∴S△PBN=![]() ,
,
∵S四边形OMPN=S△PAM+S△PBN+S平行四边形OAPB
![]()
故答案为:B


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:初中数学 来源: 题型:
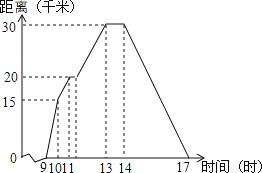
【题目】小华某天上午9时骑自行车离开家,17时回家,他有意描绘了离家的距离与时间的变化情况,如图所示.
(1)图象表示了哪两个变量的关系?哪个是自变量?哪个是因变量?
(2)10时和11时,他分别离家多远?
(3)他最初到达离家最远的地方是什么时间?离家多远?
(4)11时到13时他行驶了多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
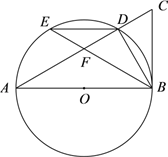
【题目】如图,AB为⊙O的直径,点D,E为⊙O上的两个点,延长AD至C,使∠CBD=∠BED.
(1)求证:BC是⊙O的切线;
(2)当点E为弧AD的中点且∠BED=30°时,⊙O半径为2,求DF的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1在正方形ABCD的外侧作两个等边三角形ADE和DCF,连接AF,BE.
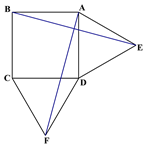
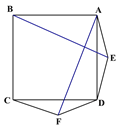

(图1) (图2) (备用图)
(1)请判断:AF与BE的数量关系是_____________,位置关系______________;
(2)如图2,若将条件“两个等边三角形ADE和DCF”变为“两个等腰三角形ADE和DCF,且EA=ED=FD=FC”,第(1)问中的结论是否仍然成立?请作出判断并给予证明;
(3)若三角形ADE和DCF为一般三角形,且AE=DF,ED=FC,第(1)问中的结论都能成立吗?请直接写出你的判断.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若八个数据x1, x2, x3, ……x8, 的平均数为8,方差为1,增加一个数据8后所得的九个数据x1, x2, x3, …x8;8的平均数![]() ________8,方差为S2 ________1.(填“>”、“=”、“<”)
________8,方差为S2 ________1.(填“>”、“=”、“<”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB、CD为两个建筑物,建筑物AB的高度为60米,从建筑物AB的顶点A点测得建筑物CD的顶点C点的俯角∠EAC为30°,测得建筑物CD的底部D点的俯角∠EAD为45°.
(1)求两建筑物底部之间水平距离BD的长度;
(2)求建筑物CD的高度(结果保留根号).
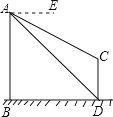
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平行四边形ABCD中,∠BAD的平分线交线段BC于点E,交线段DC的延长线于点F,以EC、CF为邻边作平行四边形ECFG.
(1)如图1,证明平行四边形ECFG为菱形;
(2)如图2,若∠ABC=90°,M是EF的中点,求∠BDM的度数;
(3)如图3,若∠ABC=120°,请直接写出∠BDG的度数.
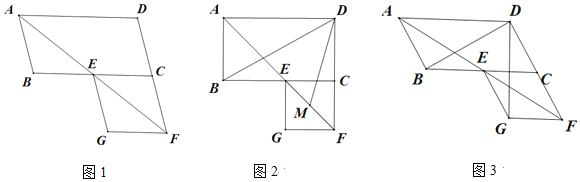
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com