
【题目】下列函数中,对于任意实数![]() ,
,![]() ,当
,当![]() 时,满足
时,满足![]() 的是( )
的是( )
A. y=﹣3x+2 B. y=2x+1 C. y=2x2+1 D. y=﹣![]()
【答案】A
【解析】分析:根据一次函数、二次函数和反比例函数图象的特点可以判断各个选项中函数图象的变化,从而可以判断各个选项是否符合题意.
详解:∵y=-3x+2,
∴y随x的增大而减小,则对于任意实数x1,x2,当x1>x2时,满足y1<y2,故选项A正确,
∵y=2x+1,
∴y随x的增大而增大,则对于任意实数x1,x2,当x1>x2时,满足y1>y2,故选项B错误,
∵y=2x2+1,
∴当x>0时,y随x的增大而增大,当x<0时,y随x的增大而减小,则对于任意实数x1,x2,当x1>x2时,足y1不一定大于y2,故选项C错误,
∵y=﹣![]() ,
,
∴y随x的增大而增大,则对于任意实数x1,x2,当x1>x2时,满足y1>y2,故选项D错误,
故选:A.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源: 题型:
【题目】如图,在数轴上A点表示数﹣2,B点表示数6,若在原点O处放一挡板,一小球甲从点A处以1个单位/秒的速度向左运动;同时另一小球乙从点B处以2个单位/秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看作一点)以原来的速度向相反的方向运动,则经过 秒,甲、乙两小球到原点的距离相等.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在RtΔABC中,AB=AC=4,∠BAC=900.点E为AB的中点,以AE为对角线作正方形ADEF,连接CF并延长交BD于点G,则线段CG的长等于________________.
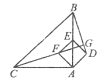
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
问题情境
如图,同学们用矩形纸片ABCD开展数学探究活动,其中AD=8,CD=6。
操作计算
(1)如图(1),分别沿BE,DF剪去RtΔABE和RtΔCDF两张纸片,如果剩余的纸片BEDF菱形,求AE的长;

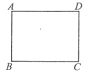
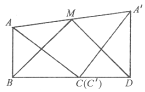
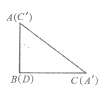
图(1) 图(2) 图(3)
操作探究
把矩形纸片ABCD沿对角线AC剪开,得到ΔABC和![]() 两张纸片
两张纸片
(2)将两张纸片如图(2)摆放,点C和![]() 重合,点B,C,D在同一条直线上,连接
重合,点B,C,D在同一条直线上,连接![]() ,记
,记![]() 的中点为M,连接BM,MD,发现ΔBMD是等腰三角形,请证明:
的中点为M,连接BM,MD,发现ΔBMD是等腰三角形,请证明:
(3)如图(3),将两张纸片叠合在一起,然后将![]() 纸片绕点B顺时针旋转a(00<a<900),连接
纸片绕点B顺时针旋转a(00<a<900),连接![]() 和
和![]() ,探究并直接写出线段
,探究并直接写出线段![]() 与
与![]() 的关系。
的关系。
查看答案和解析>>
科目:初中数学 来源: 题型:
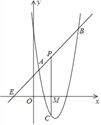
【题目】如图,直线y=x+2与抛物线y=ax2+bx+6相交于A(![]() ,
,![]() )和B(4,m),点P是AB上的动点,设点P的横坐标为n,过点P作PC⊥x轴,交抛物线于点C,与x轴交于M点.
)和B(4,m),点P是AB上的动点,设点P的横坐标为n,过点P作PC⊥x轴,交抛物线于点C,与x轴交于M点.
(1)求抛物线的表达式;
(2)点P是线段AB上异于A,B的动点,是否存在这样的点P,使线段PC的长有最大值?若存在,求出这最大值,若不存在,请说明理由;
(3)点P在直线AB上自由移动,当三个点C,P,M中恰有一点是其它两点所连线段的中点时,请直接写出m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五一小长假,李军与张明相约去宁波旅游,李军从温岭北上沿海高速,同时张明从玉环芦浦上沿海高速,温岭北与玉环芦浦相距44千米,两人约好在三门服务区集合,李军由于离三门近,行驶了1.2小时先到达三门服务站等候张明,张明走了1.4小时到达三门服务站。在整个过程中,两人均保持各自的速度匀速行驶,两人相距的路程y千米与张明行驶的时间x小时的关系如图所示,下列说法错误的是( )
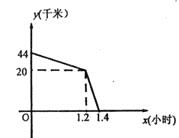
A.李军的速度是80千米/小时
B.张明的速度是100千米/小时
C.玉环芦浦至三门服务站的路程是140千米
D.温岭北至三门服务站的路程是44千米
查看答案和解析>>
科目:初中数学 来源: 题型:
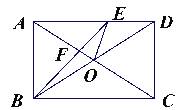
【题目】如图,在矩形ABCD中,对角线AC、BD交于点O,BE平分∠ABC交AC于点F,交AD于点E,且∠DBF=15°,求证:(1)AO=AE; (2)∠FEO的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
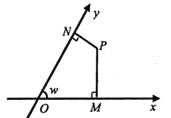
【题目】定义:在同一平面内画两条相交、有公共原点的数轴x轴和y轴,交角a≠90°,这样就在平面上建立了一个斜角坐标系,其中w叫做坐标角,对于坐标平面内任意一点P,过P作y轴和x轴的平行线,与x轴、y轴相交的点的坐标分别是a和b,则称点P的斜角坐标为(a,b).如图,w=60°,点P的斜角坐标是(1,2),过点P作x轴和y轴的垂线,垂足分别为M、N,则四边形OMPN的面积是( )
A.![]() B.
B.![]() C.
C.![]() D.3
D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一只甲虫在 5×5 的方格(每小格边长为 1)上沿着网格线运动.它从 A处出发去看望 B、C、D 处的其它甲虫,规定:向上向右走为正,向下向左走为负.如果从 A 到 B 记为:A→B(+1,+4),从 B 到 A 记为:B→A(﹣1,﹣4),其中第一个数表示左右方向,第二个数表示上下方向,那么图中
(1)A→C( , ),B→C( , ),C→D ( , );
(2)若这只甲虫的行走路线为 A→B→C→D,请计算该甲虫走过的最少路程;
(3)若这只甲虫从 A 处去甲虫 P 处的行走路线依次为(+2,+2),(+2,﹣1),(﹣2,+3),(﹣1,﹣2),请在图中标出 P 的位置.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com