
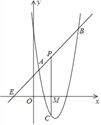
【题目】如图,直线y=x+2与抛物线y=ax2+bx+6相交于A(![]() ,
,![]() )和B(4,m),点P是AB上的动点,设点P的横坐标为n,过点P作PC⊥x轴,交抛物线于点C,与x轴交于M点.
)和B(4,m),点P是AB上的动点,设点P的横坐标为n,过点P作PC⊥x轴,交抛物线于点C,与x轴交于M点.
(1)求抛物线的表达式;
(2)点P是线段AB上异于A,B的动点,是否存在这样的点P,使线段PC的长有最大值?若存在,求出这最大值,若不存在,请说明理由;
(3)点P在直线AB上自由移动,当三个点C,P,M中恰有一点是其它两点所连线段的中点时,请直接写出m的值.
【答案】(1) y=2x2﹣8x+6;(2)见解析;(3) n的值为![]() 或
或![]() .
.
【解析】分析:(1)把B(4,m)代入y=x+2中求出m得到B(4,6),然后把A点和B点坐标代入y=ax2+bx+6得到关于a、b的方程组,再解方程组即可得到抛物线解析式;
(2)设P的坐标为(n,n+2)(![]() <n<4),则点C的坐标为(n,2n2-8n+6),用n表示PC得到PC=(n+2)-(2n2-8n+6),然后根据二次函数的性质解决问题;
<n<4),则点C的坐标为(n,2n2-8n+6),用n表示PC得到PC=(n+2)-(2n2-8n+6),然后根据二次函数的性质解决问题;
(3)设P的坐标为(n,n+2),则点C的坐标为(n,2n2-8n+6),讨论:若M点为PC的中点,则PM=CM,即n+2=-(2n2-8n+6);若P点为CM的中点,则PM=PC,即2n2-8n+6=2(x+2);若C点为PM的中点,则PC=CM,即n+2=2(2n2-8n+6),然后分别解方程可确定满足条件的n的值.
详解:
(1)∵B(4,m)在直线y=x+2上,
∴m=6,则B(4,6),
∵A(![]() ,
,![]() )、B(4,6)在抛物线y=ax2+bx+6上,
)、B(4,6)在抛物线y=ax2+bx+6上,
∴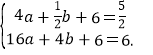 解得
解得![]() ,
,
∴所求抛物线的表达式为y=2x2﹣8x+6;
(2)设P的坐标为(n,n+2)(![]() <n<4),则点C的坐标为(n,2n2﹣8n+6),
<n<4),则点C的坐标为(n,2n2﹣8n+6),
∴PC=(n+2)﹣(2n2﹣8n+6)=﹣2n2+9n﹣4=﹣2(n﹣![]() )2+
)2+![]() ,
,
∵a=﹣2<0,
∴当n=![]() 时,线段PC取得最大值
时,线段PC取得最大值![]() ;
;
(3)设P的坐标为(n,n+2),则点C的坐标为(n,2n2﹣8n+6),
若M点为PC的中点,则PM=CM,即n+2=﹣(2n2﹣8n+6),整理得2n2﹣7n+8=0,此方程没有实数解;
若P点为CM的中点,则PM=PC,即2n2﹣8n+6=2(x+2),整理得n2﹣5n+5=0,解得n1=![]() ,n2=
,n2=![]() ;
;
若C点为PM的中点,则PC=CM,即n+2=2(2n2﹣8n+6),整理得4n2﹣17n+10=0,解得n1=![]() ,n2=
,n2=![]() ;
;
综上所述,n的值为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在长方形OABC中,O为平面直角坐标系的原点,点A坐标为(a,0),点C的坐标为(0,b),且a、b满足![]() +|b-6|=0,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O-C-B-A-O的线路移动.
+|b-6|=0,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O-C-B-A-O的线路移动.
(1)a=______________,b=_____________,点B的坐标为_______________;
(2)当点P移动4秒时,请指出点P的位置,并求出点P的坐标;
(3)在移动过程中,当点P到x轴的距离为5个单位长度时,求点P移动的时间.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数分别填入相应的集合里:
﹣|﹣5|, 2.626 626 662…, 0, ﹣π, ﹣![]() , 0.12, ﹣(﹣6).
, 0.12, ﹣(﹣6).
(1)正有理数集合:{ ____________ …};
(2)负数集合:{ ____________ …};
(3)整数集合:{ ____________ …};
(4)分数集合:{ ____________ …}.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),一平面直角坐标第xOy中,直线![]() 与y轴相交于点A,与反比例函数
与y轴相交于点A,与反比例函数![]() (x>0)的图像相交于点B(m,2)
(x>0)的图像相交于点B(m,2)
(1)求反比例函数的表达式;
(2)若将直线![]() 向上平移4个单位长度后与y轴交于点C,求ΔABC的面积;
向上平移4个单位长度后与y轴交于点C,求ΔABC的面积;
(3)如图(2)将直线![]() 向上平移,与反比例函数的图像交于点D,连接DA,DB.若
向上平移,与反比例函数的图像交于点D,连接DA,DB.若
ΔABC的面积为3,求平移后直线的表达式。


图(1) 图(2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国南宋著名数学家秦九韶的著作《数书九章》里记载有这样一道题:“问有沙田一块,有三斜,其中小斜五里,中斜十二里,大斜十三里,欲知为田几何?”这道题讲的是:有一块三角形沙田,三条边长分别为5里,12里,13里,问这块沙田面积有多大?题中“里”是我国市制长度单位,1里=500米,则该沙田的面积为( )
A.750平方千米B.75平方千米C.15平方千米D.7.5平方千米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究
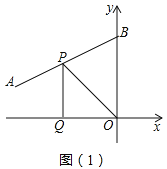
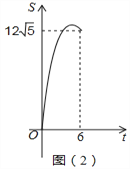
如图(1),线段AB的两个端点的坐标分别为(-12,4)(0,10),点P从点B出发,沿BA方向匀速向点A运动;同时,点Q从坐标原点O出发,沿x轴的反方向以相同的速度运动,当点P到达点A时,P,Q两点同时停止运动,设运动的时间为t秒,ΔOPQ的面积S(平方单位)与时间t(秒)之间的函数图象如图(2)所示。
(1)求点P的运动速度;
(2)求面积S与t的函数关系式及当S最最大值时点P的坐标;
(3)点P是S取最大值时的点,设点M为x轴上的点,点N为坐标平面内的点,以点O,P,M,N为顶点的四边形地矩形,请直接写出点N的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
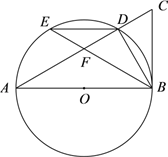
【题目】如图,AB为⊙O的直径,点D,E为⊙O上的两个点,延长AD至C,使∠CBD=∠BED.
(1)求证:BC是⊙O的切线;
(2)当点E为弧AD的中点且∠BED=30°时,⊙O半径为2,求DF的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王达和李力是八(2)班运动素质最好的两位同学,为了选出一名同学参加全校的体育运动大寒,班主任针对学校要测试的五个项目,对两位同学进行相应的测试(成绩:分),结果如下:
姓名 | 力量 | 速度 | 耐力 | 柔韧 | 灵敏 |
王达 | 60 | 75 | 100 | 90 | 75 |
李力 | 70 | 90 | 80 | 80 | 80 |
根据以上测试结果解答下列问题:
(1)补充完成下表:
姓名 | 平均成绩(分) | 中位数(分) | 众数(分) | 方差(分2) |
王达 | 80 | 75 | 75 | 190 |
李力 |
(2)任选一个角度分析推选哪位同学参加学校的比赛比较合适?并说明理由;
(3)若按力量:速度:耐力:柔韧:灵敏=1:2:3:3:1的比例折合成综合分数,推选得分同学参加比赛,请通过计算说明应推选哪位同学去参赛。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com