
【题目】综合与实践
问题情境
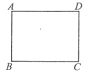
如图,同学们用矩形纸片ABCD开展数学探究活动,其中AD=8,CD=6。
操作计算
(1)如图(1),分别沿BE,DF剪去RtΔABE和RtΔCDF两张纸片,如果剩余的纸片BEDF菱形,求AE的长;

图(1) 图(2) 图(3)
操作探究
把矩形纸片ABCD沿对角线AC剪开,得到ΔABC和![]() 两张纸片
两张纸片
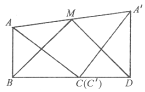
(2)将两张纸片如图(2)摆放,点C和![]() 重合,点B,C,D在同一条直线上,连接
重合,点B,C,D在同一条直线上,连接![]() ,记
,记![]() 的中点为M,连接BM,MD,发现ΔBMD是等腰三角形,请证明:
的中点为M,连接BM,MD,发现ΔBMD是等腰三角形,请证明:
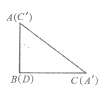
(3)如图(3),将两张纸片叠合在一起,然后将![]() 纸片绕点B顺时针旋转a(00<a<900),连接
纸片绕点B顺时针旋转a(00<a<900),连接![]() 和
和![]() ,探究并直接写出线段
,探究并直接写出线段![]() 与
与![]() 的关系。
的关系。
【答案】(1)AE的长为![]() ;(2)见解析;(3)
;(2)见解析;(3)![]()
【解析】试题分析:(1)由矩形的性质得出AB=CD=6,∠A=90°,由菱形的性质得出BE=DE=AD-AE=8-AE,在Rt△ABE中,由勾股定理得出方程,解方程即可;
(2)连接MC,证出△ACA’是等腰直角三角形,得出∠CA’A=45°,由直角三角形斜边上的中线性质和等腰三角形的性质得出A’M=CM=AM,∠MCA=45°,CM⊥AA’,证出∠BCM=∠DA’M,由SAS证明△BCM≌△DA’M,得出BM=DM,∠BMC=∠DMA’,由角的雇佣关系证出∠BMD=90°,即可得出结论;
(3)延长AC’、A’C交于点M,由旋转的性质得:BC’=BA,BA’=BC,∠A’BC=∠ABC,∠BA’C=∠BC’A,证出∠BAC=∠BC’A=∠BCA’=∠BA’C,由四边形内角和定理得出∠A’BC’+∠M=180°,证出∠M=90°,得出AC’⊥A’C,证明△ABC’∽△C’BA’,得出对应边成比例![]() ,即可求得AC’=
,即可求得AC’=![]() A’C.
A’C.
试题解析:
(1)解:∵四边形ABCD是矩形,AD=8,CD=6,
∴AB=CD=6,∠A=90°,
∵四边形BEDF是菱形,
∴BE=DE=AD-AE=8-AE,
在Rt△ABE中,由勾股定理得:AB2+AE2=BE2,
即62+AE2=(8-AE)2,
解得:AE=![]() ;
;
(2)证明:连接MC,如图2所示:
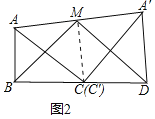
根据题意得:△ABC≌△CDA’,∠CDA’=90°,
∴AC=A’C,∠BCA=∠CA’D,∠CA’D+∠A’CD=90°,
∴∠BCA+∠A’CD=90°,
∵点B,C,D在同一条直线上,
∴∠ACA’=90°,
∴△ACA’是等腰直角三角形,
∴∠CA’A=45°,
∵M是AA’的中点,
∴A’M=CM=AM,∠MCA=45°,CM⊥AA’,
∵∠BCA=∠CA’D,
∴∠BCA+∠MCA=∠CA’D+∠CA’A,
∴∠BCM=∠DA’M,
在△BCM和△DA’M中,
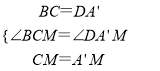
∴△BCM≌△DA’M(SAS),
∴BM=DM,∠BMC=∠DMA’,
∵∠CMD+∠DMA’=90°,
∴∠CMD+∠BMC=90°,
∴∠BMD=90°,
∴△BMD是等腰直角三角形;
(3)解:AC’⊥A’C,AC’=![]() A’C,理由如下:
A’C,理由如下:
延长AC’、A’C交于点M,如图3所示:
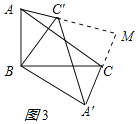
由旋转的性质得:BC’=BA,BA’=BC,∠A’BC=∠ABC,∠BA’C=∠BC’A,
∴∠BAC=∠BC’A,∠BCA’=∠BA’C,
∴∠BAC=∠BC’A=∠BCA’=∠BA’C,
∵∠BC’A+∠BC’M=180°,
∴∠BA’C+∠BC’M=180°,
∴∠A’BC’+∠M=180°,
∵∠A’BC’=∠ABC=90°,
∴∠M=90°,
∴AC’⊥A’C,
∵∠BAC=∠BC’A=∠BCA’=∠BA’C,
∴△ABC’∽△C’BA’,
∴![]() ,
,
∴AC’=![]() A’C.
A’C.


科目:初中数学 来源: 题型:
【题目】党的十八大提出,倡导富强、民主、文明、和谐,倡导自由、平等、公正、法治,倡导爱国、敬业、诚信、友善,积极培育和践行社会主义核心价值观,这24个字是社会主义核心价值观的基本内容.其中:
“富强、民主、文明、和谐”是国家层面的价值目标;
“自由、平等、公正、法治”是社会层面的价值取向;
“爱国、敬业、诚信、友善”是公民个人层面的价值准则.

小光同学将其中的“文明”、“和谐”、“自由”、“平等”的文字分别贴在4张硬纸板上,制成如右图所示的卡片.将这4张卡片背面朝上洗匀后放在桌子上,从中随机抽取一张卡片,不放回,再随机抽取一张卡片.
(1)小光第一次抽取的卡片上的文字是国家层面价值目标的概率是 ;
(2)请你用列表法或画树状图法,帮助小光求出两次抽取卡片上的文字一次是国家层面价值目标、一次
是社会层面价值取向的概率(卡片名称可用字母表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
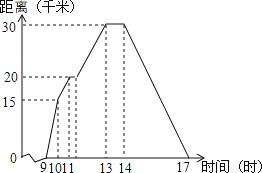
【题目】小华某天上午9时骑自行车离开家,17时回家,他有意描绘了离家的距离与时间的变化情况,如图所示.
(1)图象表示了哪两个变量的关系?哪个是自变量?哪个是因变量?
(2)10时和11时,他分别离家多远?
(3)他最初到达离家最远的地方是什么时间?离家多远?
(4)11时到13时他行驶了多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
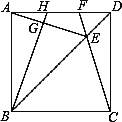
【题目】如图,在正方形ABCD中,E是对角线BD上一点,且满足BE=BC.连接CE并延长交AD于点F,连接AE,过B点作BG⊥AE于点G,延长BG交AD于点H.在下列结论中:
①AH=DF; ②∠AEF=45°; ③S四边形EFHG=S△DEF+S△AGH,
其中正确的结论有_____________________.(填正确的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),一平面直角坐标第xOy中,直线![]() 与y轴相交于点A,与反比例函数
与y轴相交于点A,与反比例函数![]() (x>0)的图像相交于点B(m,2)
(x>0)的图像相交于点B(m,2)
(1)求反比例函数的表达式;
(2)若将直线![]() 向上平移4个单位长度后与y轴交于点C,求ΔABC的面积;
向上平移4个单位长度后与y轴交于点C,求ΔABC的面积;
(3)如图(2)将直线![]() 向上平移,与反比例函数的图像交于点D,连接DA,DB.若
向上平移,与反比例函数的图像交于点D,连接DA,DB.若
ΔABC的面积为3,求平移后直线的表达式。


图(1) 图(2)
查看答案和解析>>
科目:初中数学 来源: 题型:
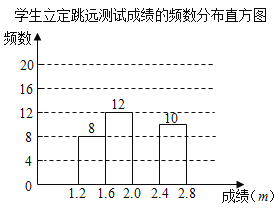
【题目】为了解某校八年级学生立定跳远水平,随机抽取该年级50名学生进行测试,并把测试成绩(单位:![]() )绘制成不完整的频数分布表和频数分布直方图.
)绘制成不完整的频数分布表和频数分布直方图.
学生立定路远测试成绩的频数分布表
分组 | 频数 |
|
|
| 12 |
|
|
| 10 |
请根据图表中所提供的信息,完成下列问题:
(1)求表中![]() ,
,![]() 的值;
的值;
(2)请把频数分布直方图补充完整;
(3)该校八年级共有800名学生,估计该年级学生立定跳远成绩在![]() 范围内的学生有多少人?
范围内的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
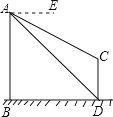
【题目】如图,AB、CD为两个建筑物,建筑物AB的高度为60米,从建筑物AB的顶点A点测得建筑物CD的顶点C点的俯角∠EAC为30°,测得建筑物CD的底部D点的俯角∠EAD为45°.
(1)求两建筑物底部之间水平距离BD的长度;
(2)求建筑物CD的高度(结果保留根号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com