
【题目】小华某天上午9时骑自行车离开家,17时回家,他有意描绘了离家的距离与时间的变化情况,如图所示.
(1)图象表示了哪两个变量的关系?哪个是自变量?哪个是因变量?
(2)10时和11时,他分别离家多远?
(3)他最初到达离家最远的地方是什么时间?离家多远?
(4)11时到13时他行驶了多少千米?
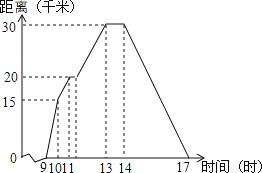
【答案】(1)图象表示离家距离与时间之间的关系,时间是自变量,离家距离是因变量;
(2)10时和11时,他分别离家15千米、20千米;
(3)他最初到达离家最远的地方是13时,离家30千米;
(4)11时到13时他行驶了:30﹣20=10千米.
【解析】
(1)根据函数图象,可得自变量、因变量;
(2)根据函数图象的纵坐标,可得答案;
(3)根据函数图象的横坐标、纵坐标,可得答案;
(4)根据函数图象的横坐标,可得函数值,根据函数值相减,可得答案;
解:(1)图象表示离家距离与时间之间的关系,时间是自变量,离家距离是因变量;
(2)10时和11时,他分别离家15千米、20千米;
(3)他最初到达离家最远的地方是13时,离家30千米;
(4)11时到13时他行驶了:30﹣20=10千米.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与双曲线相交于点A(m,3),与x轴交于点C.
与双曲线相交于点A(m,3),与x轴交于点C.
(1)求双曲线解析式;
(2)点P在x轴上,如果△ACP的面积为3,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上A点表示数﹣2,B点表示数6,若在原点O处放一挡板,一小球甲从点A处以1个单位/秒的速度向左运动;同时另一小球乙从点B处以2个单位/秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看作一点)以原来的速度向相反的方向运动,则经过 秒,甲、乙两小球到原点的距离相等.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴交于点A,与
轴交于点A,与![]() 轴交于点B,抛物线
轴交于点B,抛物线![]() 经过原点和点C(4,0),顶点D在直线AB上。
经过原点和点C(4,0),顶点D在直线AB上。
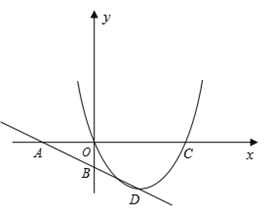
(1)求这个抛物线的解析式;
(2)在抛物线的对称轴上是否存在点P,使得以P、C、D为顶点的三角形与△ACD相似。若存在,请求出点P的坐标;若不存在,请说明理由;
(3)点Q是![]() 轴上方的抛物线上的一个动点,若
轴上方的抛物线上的一个动点,若![]() ,⊙M经过点O,C,Q,求过C点且与⊙M相切的直线解析式
,⊙M经过点O,C,Q,求过C点且与⊙M相切的直线解析式
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电业局要对某市区的电线路进行巡检,某检修小组从A地出发,在东西向的马路上检修线路,如果规定向东行驶为正,向西行驶为负,检修车一天中八次行驶记录如下:(单位:km)-4,+7,-9,+8,+6,-5,-2,-4
(1)求收工时检修小组在A地的什么方向?距A地多远?
(2)若每千米耗油0.5升,当维修小组返回到A地时,问共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四座城市A,B,C,D分别位于一个边长100km的大正方形的四个顶点,由于各城市之间的商业往来日益频繁,于是政府决定修建公路网连接它们,根据实际,公路总长设计得越短越好,公开招标的信息发布后,一个又一个方案被提交上来,经过初审后,拟从下面四个方案中选定一个再进一步认证,其中符合要求的方案是( )




A. B. C. D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在RtΔABC中,AB=AC=4,∠BAC=900.点E为AB的中点,以AE为对角线作正方形ADEF,连接CF并延长交BD于点G,则线段CG的长等于________________.
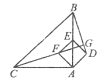
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
问题情境
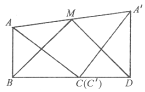
如图,同学们用矩形纸片ABCD开展数学探究活动,其中AD=8,CD=6。
操作计算
(1)如图(1),分别沿BE,DF剪去RtΔABE和RtΔCDF两张纸片,如果剩余的纸片BEDF菱形,求AE的长;

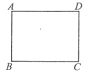
图(1) 图(2) 图(3)
操作探究
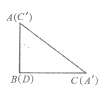
把矩形纸片ABCD沿对角线AC剪开,得到ΔABC和![]() 两张纸片
两张纸片
(2)将两张纸片如图(2)摆放,点C和![]() 重合,点B,C,D在同一条直线上,连接
重合,点B,C,D在同一条直线上,连接![]() ,记
,记![]() 的中点为M,连接BM,MD,发现ΔBMD是等腰三角形,请证明:
的中点为M,连接BM,MD,发现ΔBMD是等腰三角形,请证明:
(3)如图(3),将两张纸片叠合在一起,然后将![]() 纸片绕点B顺时针旋转a(00<a<900),连接
纸片绕点B顺时针旋转a(00<a<900),连接![]() 和
和![]() ,探究并直接写出线段
,探究并直接写出线段![]() 与
与![]() 的关系。
的关系。
查看答案和解析>>
科目:初中数学 来源: 题型:
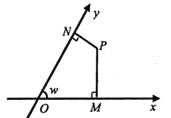
【题目】定义:在同一平面内画两条相交、有公共原点的数轴x轴和y轴,交角a≠90°,这样就在平面上建立了一个斜角坐标系,其中w叫做坐标角,对于坐标平面内任意一点P,过P作y轴和x轴的平行线,与x轴、y轴相交的点的坐标分别是a和b,则称点P的斜角坐标为(a,b).如图,w=60°,点P的斜角坐标是(1,2),过点P作x轴和y轴的垂线,垂足分别为M、N,则四边形OMPN的面积是( )
A.![]() B.
B.![]() C.
C.![]() D.3
D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com