练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

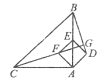
    【题目】如图，在RtΔABC中，AB=AC=4,∠BAC=900.点E为AB的中点，以AE为对角线作正方形ADEF，连接CF并延长交BD于点G，则线段CG的长等于________________.

    【答案】

    【解析】延长AF交BC于M，AB交CG于O．

    ∵AB=AC=4，∠CAB=90°，
    ∴BC=

    ∵AE=EB=2，四边形AFED是正方形，
    ∴AF=EF=

    ，∴∠EAF=∠EAD=45°，
    ∴∠MAB=∠MAC=45°，
    ∴CM=BM=AM=2

    ∴FM=AM-AF=

    在Rt△CMF中，CF＝ ＝,

    ∵AC=AB，∠CAF=∠BAD=45°，AF=AD，
    ∴△CAF≌△BAD，
    ∴∠ACF=∠ABD，
    ∵∠AOC=∠BOG，
    ∴∠CAO=∠BGO=90°，
    ∵∠MCF=∠BCG，∠CMF=∠CGB=90°，
    ∴△CMF∽△CGB，

    ∴

    ∴,

    ∴CG=.

    故答案是： .

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

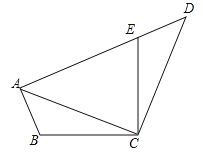
    【题目】如图，已知在四边形ABCD中，点E在AD上，∠BCE=∠ACD=90°，∠BAC=∠D，BC=CE．

    （1）求证：AC=CD；

    （2）若AC=AE，求∠DEC的度数．

    【答案】（1）证明见解析；（2）112.5°．

    【解析】试题分析： 根据同角的余角相等可得到结合条件，再加上 可证得结论；
    根据 得到 根据等腰三角形的性质得到 由平角的定义得到

    试题解析： 证明：

    在△ABC和△DEC中， ，

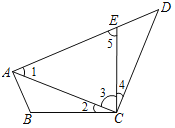
    （2）∵∠ACD＝90°，AC＝CD，

    ∴∠1＝∠D＝45°，

    ∵AE＝AC，

    ∴∠3＝∠5＝67.5°，

    ∴∠DEC＝180°－∠5＝112.5°．

    【题型】解答题
    【结束】
    21

    【题目】一个零件的形状如图所示，工人师傅按规定做得∠B=90°，

    AB＝3，BC＝4，CD＝12，AD＝13，假如这是一块钢板，你能帮工人师傅计算一下这块钢板的面积吗？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一辆货车从百货大楼出发负责送货，向东走了 5 千米到达小明家，继续向东走了 1.5 千米到达小红家，然后向西走了 9.5 千米到达小刚家，最后返回百货大楼．

    （1）以百货大楼为原点，向东为正方向，1 个单位长度表示 1 千米，请你在数轴上标出小明、小红、小刚家的位置．（小明家用点 A 表示，小红家用点 B 表示，小刚家用点 C 表示）

    （2）小明家与小刚家相距多远？

    （3）若货车每千米耗油 0.6 升，那么这辆货车此次送货共耗油多少升？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

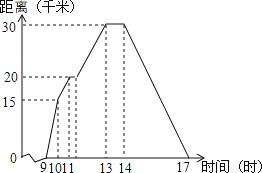
    【题目】小华某天上午9时骑自行车离开家，17时回家，他有意描绘了离家的距离与时间的变化情况，如图所示．

    （1）图象表示了哪两个变量的关系？哪个是自变量？哪个是因变量？

    （2）10时和11时，他分别离家多远？

    （3）他最初到达离家最远的地方是什么时间？离家多远？

    （4）11时到13时他行驶了多少千米？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】把下列各数分别填入相应的集合里：

    ﹣|﹣5|， 2.626 626 662…， 0， ﹣π， ﹣， 0.12， ﹣（﹣6）．

    （1）正有理数集合：{ ____________ …}；

    （2）负数集合：{ ____________ …}；

    （3）整数集合：{ ____________ …}；

    （4）分数集合：{ ____________ …}．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

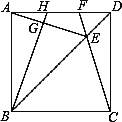
    【题目】如图，在正方形ABCD中，E是对角线BD上一点，且满足BE=BC．连接CE并延长交AD于点F，连接AE，过B点作BG⊥AE于点G，延长BG交AD于点H．在下列结论中：

    ①AH=DF； ②∠AEF=45°； ③S四边形EFHG=S△DEF+S△AGH，

    其中正确的结论有_____________________．(填正确的序号)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图（1），一平面直角坐标第xOy中，直线与y轴相交于点A，与反比例函数（x>0)的图像相交于点B（m,2)

    （1）求反比例函数的表达式；

    （2）若将直线向上平移4个单位长度后与y轴交于点C，求ΔABC的面积；

    （3）如图（2）将直线向上平移，与反比例函数的图像交于点D，连接DA,DB.若

    ΔABC的面积为3，求平移后直线的表达式。

    图（1） 图（2）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列函数中，对于任意实数，，当时，满足的是（　　）

    A. y=﹣3x+2 B. y=2x+1 C. y=2x2+1 D. y=﹣

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若八个数据x1， x2， x3， ……x8， 的平均数为8，方差为1，增加一个数据8后所得的九个数据x1， x2， x3， …x8；8的平均数________8，方差为S2 ________1．(填“>”、“=”、“<”)

    查看答案和解析>>

    同步练习册答案