
����Ŀ��һ�������Ӱٻ���¥���������ͻ��������� 5 ǧ����С���ң����������� 1.5 ǧ����С��ң�Ȼ���������� 9.5 ǧ����С�ռң���ذٻ���¥��
![]()
��1���ٻ���¥Ϊԭ�㣬��Ϊ������1 ����λ���ȱ�ʾ 1 ǧ�ף������������ϱ��С����С�졢С�ռҵ�λ������С�����õ� A ��ʾ��С����õ� B ��ʾ��С�ռ��õ� C ��ʾ��
��2��С������С�ռ�����Զ��
��3��������ÿǧ���� 0.6 ������ô���������˴��ͻ������Ͷ�������
���𰸡���1����ͼ��ʾ����������2��С������С�ռ���� 8 ǧ�ף���3�����������˴��ͻ������� 11.4 ����
��������
��1��������֪���ٻ���¥Ϊԭ�㣬����Ϊ�������� 1 ����λ���ȱ�ʾ 1 ǧ��һ�������Ӱٻ���¥������������ 5 ǧ�ף�����С���ң����������� 1 .5 ǧ����С��ң�Ȼ�������� 9.5 ǧ�ף�����С�ռң���ذٻ���¥����С���ҡ�С��Һ�С�ռ��������ϵ�λ�ÿ�֪��
��2����С���ҵ������ȥ��С�ռҵ����꼴�ɣ�
��3����������һ�����ߵ�·�̣�ʵ���Ͼ��� 5+1.5+9.5+3=19��ǧ�����������ӳ����������г̹�������=������ʻÿǧ��������������ʻ���ߵ���·�̣�
��1����ͼ��ʾ��
![]()
��2��С������С�ռ���ࣺ5������3��=8��ǧ�ף���
��С������С�ռ���� 8 ǧ�ף�
��3�����������˴��ͻ������ͣ���5+1.5+9.5+3����0.6=11.4��������
�����������˴��ͻ������� 11.4 ����


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AB=AC=24���ף�BC=16���ף���DΪAB���е㣬��P���߶�BC����4����/����ٶ���B����C���˶���ͬʱ����Q���߶�CA����C����A���˶�������Q���˶��ٶ�Ϊ_______����/��ʱ���ܹ���ijһʱ��ʹ��BPD����CQPȫ�ȣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���ı���ABCD��E��F��G��H�Ǹ��ߵ��е㣮
��1����֤���ı���EFGH��ƽ���ı��Σ�
��2�������ı���ABCD��һ�����Σ������ı���EFGH��ʲôͼ�Σ���֤����IJ��룮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������A���ʾ����2��B���ʾ��6������ԭ��O����һ���壬һС��״ӵ�A����1����λ/����ٶ������˶���ͬʱ��һС���Ҵӵ�B����2����λ/����ٶ�Ҳ�����˶������������������Ĵ�С���ɿ���һ�㣩��ԭ�����ٶ����෴�ķ����˶����� �룬�ס�����С��ԭ��ľ�����ȣ�
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��![]() ��
��![]() �ύ�ڵ�A����
�ύ�ڵ�A����![]() �ύ�ڵ�B��������
�ύ�ڵ�B��������![]() ����ԭ��͵�C��4,0��������D��ֱ��AB�ϡ�
����ԭ��͵�C��4,0��������D��ֱ��AB�ϡ�
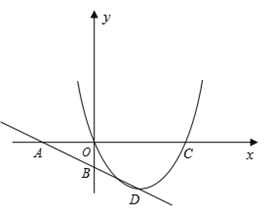
��1������������ߵĽ���ʽ��
��2���������ߵĶԳ������Ƿ���ڵ�P��ʹ����P��C��DΪ��������������ACD���ơ������ڣ��������P�����ꣻ�������ڣ���˵�����ɣ�
��3����Q��![]() ���Ϸ����������ϵ�һ�����㣬��
���Ϸ����������ϵ�һ�����㣬��![]() ����M������O��C��Q�����C�������M���е�ֱ�߽���ʽ
����M������O��C��Q�����C�������M���е�ֱ�߽���ʽ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ҵ��Ҫ��ij�����ĵ���·����Ѳ�죬ij����С���A�س������ڶ��������·�ϼ�����·������涨����ʻΪ����������ʻΪ��������һ���а˴���ʻ��¼���£�����λ��km��-4��+7��-9��+8��+6��-5��-2��-4
��1�����չ�ʱ����С����A�ص�ʲô����A�ض�Զ��
��2����ÿǧ����0.5������ά��С�鷵�ص�A��ʱ���ʹ����Ͷ�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У�AB=AC=4,��BAC=900.��EΪAB���е㣬��AEΪ�Խ�����������ADEF������CF���ӳ���BD�ڵ�G�����߶�CG�ij�����________________.
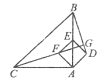
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У��Խ���AC��BD���ڵ�O��BEƽ�֡�ABC��AC�ڵ�F����AD�ڵ�E���ҡ�DBF=15������֤����1��AO=AE; (2)��FEO�Ķ���.
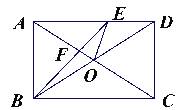
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com