练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】数学的趣味无处不在，在学习数学的过程中，小明发现了有规律的等式：

    ；

    ；

    ；

    ；

    ……

    （1）从计算过程中找出规律，可知：

    ① ；

    ② =．

    （2）计算：(结果用含n的式子表示)

    （3）对于算式：

    ①计算出算式的值（结果用乘方表示）；

    ②直接写出结果的个位数字是几？

    【答案】（1）① ；②；（2）；（3）①；②1.

    【解析】

    （1）根据前面几个式子的规律即可得出结论；

    （2）根据（1）中②可得结论；

    （3）①利用2=3－1，反复利用平方差公式计算即可；

    ②34=81，而81的正整数幂的个位数始终是1，由此得出结论．

    （1）① ；

    ②；

    （2）由（1）知：

    ∴

    当x=2时，

    所以原式=

    （3）①原式=

    =

    =

    =

    =；

    ② ．

    ∵81的正整数幂的个位数始终是1，∴原式的个位数是 1．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】（认识概念）

    点P、Q分别是两个图形G1、G2上的任意一点，当P、Q两点之间的距离最小时，我们把这个最小距离叫作图形G1、G2的亲密距离，记为d(G1，G2)．例如，如果点M、N分别是两条相交直线a、b上的任意一点，则d(a，b)＝0

    （初步运用）

    如图1，长方形四个顶点分别是点A、B、C、D，边AB＝CD＝5，AD＝BC＝3．那么d(AB，CD)＝___，d(AD，BC)＝_____，d(AD，AB)＝_____．

    （深入探究）

    (1)在图1中，如果将线段CD沿它所在直线平移(边AB不动)，且使d(CD，AB)不变，那么线段CD的中点偏离它原来位置的最大距离为______；

    (2)如图2，线段AB∥直线CD，AB＝1，点A到CD的距离为3，将线段AB绕点A旋转90°后的对应线段为AB′，则d(AB′，CD)＝______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在Rt△ABC中，B为直角，DE是AC的垂直平分线，E在BC上，∠BAE：∠BAC＝1：5，则∠C＝_________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读下列材料：

    2016年，北京市坚持创新、协调、绿色、开放、共享的发展理念，围绕首都城市战略定位，加快建设国际一流的和谐宜居之都，在教育、科技等方面保持平稳健康发展，实现了“十三五”良好开局．

    在教育方面，全市共有58所普通高校和81个科研机构培养研究生，全年研究生招生9.7万人，在校研究生29.2万人．全市91所普通高校全年招收本专科学生15.5万人，在校生58.8万人．全市成人本专科招生6.1万人，在校生17.2万人．

    在科技方面，2016年全年研究与试验发展（R&D）经费支出1479.8亿元，比2015年增长了6.9%，全市研究与试验发展（R&D）活动人员36.2万人，比上年增长1.1万人．2013年，2014年，2015年全年研究与试验发展（R&D）经费支出分别为1185.0亿元，1268.8亿元，1384.0亿元，分别比前一年度增长11.4%，7.1%，9.1%．

    （以上数据来源于北京市统计局）

    根据以上材料解答下列问题：

    （1）请用统计图或统计表将北京市2016年研究生、普通高校本专科学生、成人本专科学生的招生人数和在校生人数表示出来；

    （2）2015年北京市研究与试验发展（R&D）活动人员为 万人；

    （3）根据材料中的信息，预估2017年北京市全年研究与试验发展（R&D）经费支出约 亿元，你的预估理由是 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1在正方形ABCD的外侧作两个等边三角形ADE和DCF，连接AF，BE．

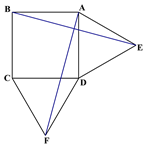
    （图1） （图2） （备用图）

    （1）请判断：AF与BE的数量关系是_____________，位置关系______________；

    （2）如图2，若将条件“两个等边三角形ADE和DCF”变为“两个等腰三角形ADE和DCF，且EA=ED=FD=FC”，第（1）问中的结论是否仍然成立？请作出判断并给予证明；

    （3）若三角形ADE和DCF为一般三角形，且AE=DF，ED=FC，第（1）问中的结论都能成立吗？请直接写出你的判断．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

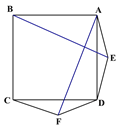
    【题目】在△ABC中，∠ACB=90°，以AB为斜边作等腰直角三角形ABD，且点D与点C在直线AB的两侧，连接CD．

    （1）如图1，若∠ABC=30°，则∠CAD的度数为________．

    （2）已知AC=1，BC=3．

    ①依题意将图2补全；

    ②求CD的长；

    （3）用等式表示线段AC，BC，CD之间的数量关系（直接写出即可）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知一次函数图像过点P(0，6)，且平行于直线y=-2x

    （1）求该一次函数的解析式

    （2）若点A(，a)、B(2，b)在该函数图像上，试判断a、b的大小关系，并说明理由。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我校4月份举办了教职工羽毛球赛，本次比赛共分三个项目：男双、女双和混双．比赛规定参赛男教师只能在男双或混双中选报一项，参赛女教师只能在女双或混双中选报一项，现将参赛人数和各项的参赛队数（两人组成一队）绘制成了如下不完整的统计图：

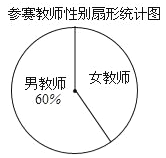
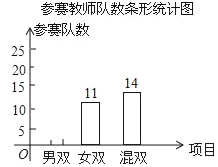
    （1）本次比赛共有_____名参赛教师，并补全条形统计图；

    （2）已知男双冠军分别是音乐教师和体育教师，女双冠军都是数学教师，混双冠军分别是数学男教师和美术女教师．暑假期问市教委将举办全市中小学教师羽毛球比赛，比赛规定：每所学校的参赛人数为两人，且参赛教师不得属于同一学科．所以学校决定：从三支冠军队伍中的数学教师中随机选取一人，再从其他教师中选取一人参加比赛．请用列表法或画树状图的方法求出所选两位教师恰好搭档参加混双项目的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

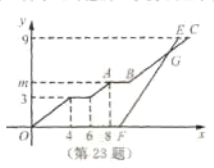
    【题目】小强与小刚都住在安康小区，在同一所学校读书．某天早上，小强从安康小区站乘坐校车去学校，途中需停靠两个站点才能到达学校站点，且每个站点停留分钟，校车行驶途中始终保持匀速．当天早上，小刚从安康小区站乘坐出租车沿相同路线出发，出租车匀速行驶，比小强乘坐的校车早分钟到学校站点．他们乘坐的车辆从安康小区站出发所行驶路程（千米）与行驶时间（分钟）之间的函数图象如图所示．

    （1）求点的纵坐标的值；

    （2）小刚乘坐出租车出发后经过多少分钟追到小强所乘坐的校车？并求此时他们距学校站点的路程．

    查看答案和解析>>

    同步练习册答案