
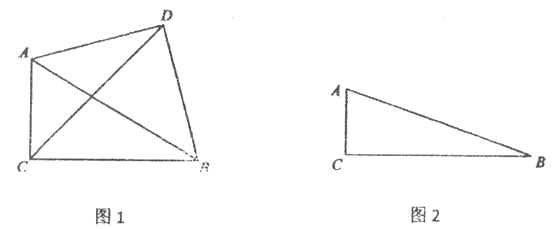
【题目】在△ABC中,∠ACB=90°,以AB为斜边作等腰直角三角形ABD,且点D与点C在直线AB的两侧,连接CD.
(1)如图1,若∠ABC=30°,则∠CAD的度数为________.
(2)已知AC=1,BC=3.
①依题意将图2补全;
②求CD的长;
(3)用等式表示线段AC,BC,CD之间的数量关系(直接写出即可).
【答案】(1)105°;(2)①答案见解析;②CD=2![]() ;(3)AC+BC=
;(3)AC+BC=![]() CD.
CD.
【解析】试题分析:(1)先判断出∠CAD=∠DBE,再利用等腰直角三角形求出∠ABD=45°,进而求出∠CBD,最后用邻补角即可得出结论;
(2)①根据题意及基本作图即可补全图形;
②构造出△ACD≌△BED,进而判断出△CDE是等腰直角三角形,再利用等腰直角三角形的性质即可得出解;
构造出△BDH≌△ADG,进而判断出△CDH是等腰直角三角形,再利用等腰直角三角形的性质即可得出结论;
(3)同(2)的方法即可得出结论.
试题解析:
(1)∵∠ACB=∠ADB=90°,
∴∠CAD+∠CBD═180°.
∵∠DBE+∠CBD═180°,
∴∠CAD=∠DBE.
∵△ADB是等腰直角三角形,
∴∠ABD=45°,
∵∠ABC=30°,
∴∠CBD=∠ABD+∠ABC=75°,
∴∠CAD=∠DBE=180°-75°=105°
故答案为:105°.
(2)①补全图形,如图所示.
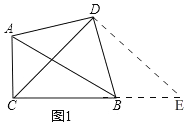
②如图2,
∵∠ACB=∠ADB=90°,
∴∠CAD+∠CBD═180°.
∵∠DBE+∠CBD═180°,
∴∠CAD=∠DBE.
∵DA=DB,AC=BE,
∴△ACD≌△BED.
∴DC=DE,∠ADC=∠BDE.
∴∠CDE=90°.
∴△CDE为等腰直角三角形.
∵AC=1,BC=3,
∴CE=4.
∴CD=2![]() .
.
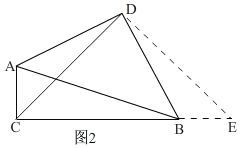
如图2,
∵∠ACB=∠ADB=90°,
∴∠CAD+∠CBD═180°.
∵∠DAG+∠CAD═180°,
∴∠CBD=∠DAG.
∵DA=DB,∠DGA=∠DHB=90°,
∴△BDH≌△ADG.
∴DH=DG,BH=AG.
∴∠DCH=∠DCG=45°.
∴△CHD为等腰直角三角形.
∵AC=1,BC=3,
∴CH=2.
∴CD=2![]() .
.
(3)AC+BC=![]() CD,
CD,
理由:如图2,
∵∠ACB=∠ADB=90°,
∴∠CAD+∠CBD═180°.
∵∠DBE+∠CBD═180°,
∴∠CAD=∠DBE.
∵DA=DB,AC=BE,
∴△ACD≌△BED.
∴DC=DE,∠ADC=∠BDE.
∴∠CDE=90°.
∴△CDE为等腰直角三角形.
∴CE=![]() CD,
CD,
∵CE=BC+BE=BC+AC.
即:AC+BC=![]() CD.
CD.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】(1)方法回顾
在学习三角形中位线时,为了探索三角形中位线的性质,思路如下:
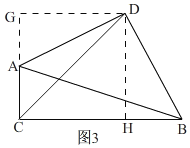
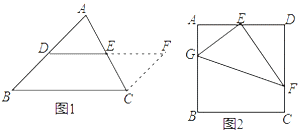
第一步添加辅助线:如图1,在△ABC中,延长DE (D、E分别是AB、AC的中点)到点F,使得EF=DE,连接CF;
第二步证明△ADE≌△CFE,再证四边形DBCF是平行四边形,从而得到DE∥BC,DE=![]() BC.
BC.
(2)问题解决
如图2,在正方形ABCD中,E为AD的中点,G、F分别为AB、CD边上的点,若AG=2,DF=3,∠GEF=90°,求GF的长.
(3)拓展研究
如图3,在四边形ABCD中,∠A=100°,∠D=110°,E为AD的中点,G、F分别为AB、CD边上的点,若AG=4,DF=![]() ,∠GEF=90°,求GF的长.
,∠GEF=90°,求GF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边分别交CB,DC(或它们的延长线)于点M,N.当∠MAN绕点A旋转到BM=DN时(如图1),易证BM+DN=MN.

(1)当∠MAN绕点A旋转到BM≠DN时(如图2),线段BM,DN和MN之间有怎样的数量关系?写出猜想,并加以证明.
(2)当∠MAN绕点A旋转到如图3的位置时,线段BM,DN和MN之间又有怎样的数量关系?请直接写出你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线l1∥l2∥l3∥l4,相邻两条平行线间的距离都是1,正方形ABCD的四个顶点分别在四条直线上,则正方形ABCD的面积为( )

A. ![]() B.
B. ![]() C. 3 D. 5
C. 3 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学的趣味无处不在,在学习数学的过程中,小明发现了有规律的等式:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
……
(1)从计算过程中找出规律,可知:
①![]() ;
;
② =![]() .
.
(2)计算:![]() (结果用含n的式子表示)
(结果用含n的式子表示)
(3)对于算式:![]()
①计算出算式的值(结果用乘方表示);
②直接写出结果的个位数字是几?
查看答案和解析>>
科目:初中数学 来源: 题型:
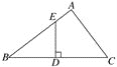
【题目】已知,如图,在△ABC中,D是BC的中点,DE⊥BC,垂足为D,交AB于点E,且BE2-EA2=AC2,
(1)求证:∠A=90°.
(2)若DE=3,BD=4,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】经过建设者三年多艰苦努力地施工,贯通我市A、B两地又一条高速公路全线通车.已知原来A地到B地普通公路长150km,高速公路路程缩短了30km,如果一辆小车从A地到B地走高速公路的平均速度可以提高到原来的1.5倍,需要的时间可以比原来少用1小时.求小车走普通公路的平均速度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知⊙O是以AB为直径的△ABC的外接圆,过点A作⊙O的切线交OC的延长线于点D,交BC的延长线于点E.
(1)求证:∠DAC=∠DCE;
(2)若AE=ED=2,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,某超市从一楼到二楼的电梯![]() 的长为16. 50 m,坡角
的长为16. 50 m,坡角![]() 为32°.
为32°.
(1)求一楼与二楼之间的高度![]() (精确到0. 01 m) ;
(精确到0. 01 m) ;
(2)电梯每级的水平级宽均是0.25m,如图②,小明跨上电梯时,该电梯以每秒上升2级
的高度运行,10s后他上升了多少米?
(精确到0. 01 m,参考数据: ![]() )
)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com