
【题目】(1)方法回顾
在学习三角形中位线时,为了探索三角形中位线的性质,思路如下:
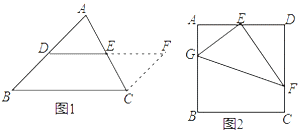
第一步添加辅助线:如图1,在△ABC中,延长DE (D、E分别是AB、AC的中点)到点F,使得EF=DE,连接CF;
第二步证明△ADE≌△CFE,再证四边形DBCF是平行四边形,从而得到DE∥BC,DE=![]() BC.
BC.
(2)问题解决
如图2,在正方形ABCD中,E为AD的中点,G、F分别为AB、CD边上的点,若AG=2,DF=3,∠GEF=90°,求GF的长.
(3)拓展研究
如图3,在四边形ABCD中,∠A=100°,∠D=110°,E为AD的中点,G、F分别为AB、CD边上的点,若AG=4,DF=![]() ,∠GEF=90°,求GF的长.
,∠GEF=90°,求GF的长.

【答案】问题解决:GF=5;拓展研究:GF=![]() .
.
【解析】
(1)延长GE、FD交于点H,可证得△AEG≌△DEH,结合条件可证明EF垂直平分GH,可得GF=FH,可求得GF的长;
(2)过点D作AB的平行线交GE的延长线于点H,过H作CD的垂线,垂足为P,连接HF,可证明△AEG≌△DEH,结合条件可得到△HPD为等腰直角三角形,可求得PF的长,在Rt△HFP中,可求得HF,则可求得GF的长.
(1)如图2,延长GE、FD交于点H,
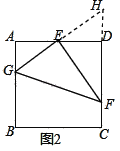
∵E为AD中点,
∴EA=ED,且∠A=∠EDH=90°,
在△AEG和△DEH中,
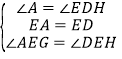
∴△AEG≌△DEH(ASA),
∴AG=HD=2,EG=EH,
∵∠GEF=90°,
∴EF垂直平分GH,
∴GF=HF=DH+DF=2+3=5;
(2)如图3,过点D作AB的平行线交GE的延长线于点H,过H作CD的垂线,垂足为P,连接HF,
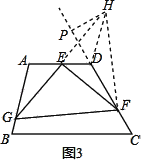
同(1)可知△AEG≌△DEH,GF=HF,
∴∠A=∠HDE=100°,AG=HD=4,
∵∠ADC=110°,
∴∠HDF=360°﹣100°﹣110°=150°,
∴∠HDP=30°,∴HP=2,
PD=PH=![]() ,
,
∴PF=PD+DF=![]()
在Rt△HFP中,∠HPF=90°,HP=2,PF=![]() ,
,
∴HF=![]() =
=![]() ,
,
∴GF=![]() .
.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AB∥DC,∠B=90°,F为DC上一点,且FC=AB,E为AD上一点,EC交AF于点G.
(1)求证:四边形ABCF是矩形;
(2)若EA=EG,求证:ED=EC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=1,AD=2,点E是边AD上的一个动点,把△BAE沿BE折叠,点A落在A′处,如果A′恰在矩形的对称轴上,则AE的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,所有小正方形的边长都为1个单位,A、B、C均在格点上.

(1)过点C画线段AB的平行线CD;
(2)过点A画线段BC的垂线,垂足为E;
(3)线段AE的长度是点 到直线 的距离;
(4)比较线段AE、AB、BC的大小关系(用“<”连接).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(认识概念)
点P、Q分别是两个图形G1、G2上的任意一点,当P、Q两点之间的距离最小时,我们把这个最小距离叫作图形G1、G2的亲密距离,记为d(G1,G2).例如,如果点M、N分别是两条相交直线a、b上的任意一点,则d(a,b)=0
(初步运用)
如图1,长方形四个顶点分别是点A、B、C、D,边AB=CD=5,AD=BC=3.那么d(AB,CD)=___,d(AD,BC)=_____,d(AD,AB)=_____.
(深入探究)
(1)在图1中,如果将线段CD沿它所在直线平移(边AB不动),且使d(CD,AB)不变,那么线段CD的中点偏离它原来位置的最大距离为______;
(2)如图2,线段AB∥直线CD,AB=1,点A到CD的距离为3,将线段AB绕点A旋转90°后的对应线段为AB′,则d(AB′,CD)=______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB为⊙O的直径,BD和CD为⊙O的切线,切点分别为B和C.
(1)求证:AC∥OD;
(2)当BC=BD,且BD=6cm时,求图中阴影部分的面积(结果不取近似值).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题发现
如图1,四边形ABCD为矩形,AB=a,BC=b,点P在矩形ABCD的对角线AC上,Rt△PEF的两条直角边PE,PF分别交BC,DC于点M,N,当PM⊥BC,PN⊥CD时,![]() = (用含a,b的代数式表示).
= (用含a,b的代数式表示).
(2)拓展探究
在(1)中,固定点P,使△PEF绕点P旋转,如图2,![]() 的大小有无变化?请仅就图2的情形给出证明.
的大小有无变化?请仅就图2的情形给出证明.
(3)问题解决
如图3,四边形ABCD为正方形,AB=BC=a,点P在对角线AC上,M,N分别在BC,CD上,PM⊥PN,当AP=nPC时,(n是正实数),直接写出四边形PMCN的面积是 (用含n,a的代数式表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() (a≠0)的对称轴为直
(a≠0)的对称轴为直![]() =1,与
=1,与![]() 轴的一个交点坐标为(-1,0),其部分图象如图所示.下列结论:①
轴的一个交点坐标为(-1,0),其部分图象如图所示.下列结论:① ![]() ;②方程
;②方程![]() =0的两个根是
=0的两个根是![]() ,
,![]() ; ③
; ③![]() ;④当
;④当![]() 时,
时,![]() 的取值范围是
的取值范围是![]() ;⑤当x1<x2<0时,y1<y2.其中结论正确的个数是( )
;⑤当x1<x2<0时,y1<y2.其中结论正确的个数是( )
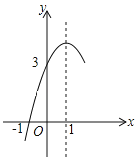
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠ACB=90°,以AB为斜边作等腰直角三角形ABD,且点D与点C在直线AB的两侧,连接CD.
(1)如图1,若∠ABC=30°,则∠CAD的度数为________.
(2)已知AC=1,BC=3.
①依题意将图2补全;
②求CD的长;
(3)用等式表示线段AC,BC,CD之间的数量关系(直接写出即可).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com