
【题目】如图,四边形ABCD中,AB∥DC,∠B=90°,F为DC上一点,且FC=AB,E为AD上一点,EC交AF于点G.
(1)求证:四边形ABCF是矩形;
(2)若EA=EG,求证:ED=EC.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某商场用14500元购进甲、乙两种矿泉水共500箱,矿泉水的成本价与销售价如表(二)所示:
类别 | 成本价(元/箱) | 销售价(元/箱) |
甲 | 25 | 35 |
乙 | 35 | 48 |
求:(1)购进甲、乙两种矿泉水各多少箱?
(2)该商场售完这500箱矿泉水,可获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知平面内有A、B、C、D四点,请按下列要求作图.

(1)作射线AC,线段DC;
(2)作∠BAD的补角,并标上字母;
(3)用量角器量出∠BAC的度数,并求出它的余角的度数(精确到度);
(4)在图中求作一点P,使P点到A、B、C、D四点的距离和最短.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上有A、B两点(点A在点B的左侧),且两点距离为8个单位长度,动点P从点A出发,以每秒2个单位长度的速度沿数轴向右匀速运动,设运动时间为t(t>0)秒.
![]()
(1)图中如果点A、B表示的数是互为相反数,那么点A表示的数是 ;
(2)当t=3秒时,点A与点P之间的距离是 个长度单位;
(3)当点A表示的数是-3时,用含t的代数式表示点P表示的数;
(4)若点P到点A的距离是点P到点B的距离的2倍,请直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,二次函数y=﹣![]() x2+bx+c的图线与坐标轴分别交于点A、B、C,其中点A(0,8),OB=
x2+bx+c的图线与坐标轴分别交于点A、B、C,其中点A(0,8),OB=![]() OA.
OA.
(1)求二次函数的表达式;
(2)若OD=OB,点F为该二次函数在第二象限内图象上的动点,E为DF的中点,当△CEF的面积最大时,求出点E的坐标;
(3)将三角形CEF绕E旋转180°,C点落在M处,若M恰好在该抛物线上,求出此时△CEF的面积.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)方法回顾
在学习三角形中位线时,为了探索三角形中位线的性质,思路如下:
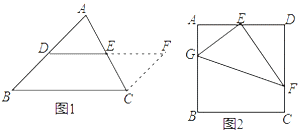
第一步添加辅助线:如图1,在△ABC中,延长DE (D、E分别是AB、AC的中点)到点F,使得EF=DE,连接CF;
第二步证明△ADE≌△CFE,再证四边形DBCF是平行四边形,从而得到DE∥BC,DE=![]() BC.
BC.
(2)问题解决
如图2,在正方形ABCD中,E为AD的中点,G、F分别为AB、CD边上的点,若AG=2,DF=3,∠GEF=90°,求GF的长.
(3)拓展研究
如图3,在四边形ABCD中,∠A=100°,∠D=110°,E为AD的中点,G、F分别为AB、CD边上的点,若AG=4,DF=![]() ,∠GEF=90°,求GF的长.
,∠GEF=90°,求GF的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com