
【题目】如图,已知⊙O是以AB为直径的△ABC的外接圆,过点A作⊙O的切线交OC的延长线于点D,交BC的延长线于点E.
(1)求证:∠DAC=∠DCE;
(2)若AE=ED=2,求⊙O的半径.

【答案】(1)证明见解析;(2)⊙O的半径为![]()
【解析】分析:(1)由切线的性质可知∠DAB=90°,由直角所对的圆周为90°可知∠ACB=90°,根据同角的余角相等可知∠DAC=∠B,然后由等腰三角形的性质可知∠B=∠OCB,由对顶角的性质可知∠DCE=∠OCB,故此可知∠DAC=∠DCE;
(2)先证明△DCE∽△DAC,求出CD的长,设⊙O的半径为x,则OA=OC=x,在Rt△OAD中,由勾股定理列方程即可求出半径的长.
详解:证明:(1)AD是⊙O的切线,
∴∠DAB=90°,即∠DAC+∠CAB=90°,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠CAB+∠ABC=90°,
∴∠DAC=∠B,
∵OC=OB,
∴∠B=∠OCB=∠DAC,
又∵∠DCE=∠OCB,
∴∠DAC=∠DCE;
解:(2) ∵∠DAC=∠DCE, ∠D=∠D,
∴△DCE∽△DAC,
∴![]() 即
即![]() ,
,
∴DC=![]() .
.
设⊙O的半径为x,则OA=OC=x,
在Rt△OAD中,由勾股定理,得
![]() ,
,
解得x =![]() ,
,
答:⊙O的半径为![]() 。
。


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() (a≠0)的对称轴为直
(a≠0)的对称轴为直![]() =1,与
=1,与![]() 轴的一个交点坐标为(-1,0),其部分图象如图所示.下列结论:①
轴的一个交点坐标为(-1,0),其部分图象如图所示.下列结论:① ![]() ;②方程
;②方程![]() =0的两个根是
=0的两个根是![]() ,
,![]() ; ③
; ③![]() ;④当
;④当![]() 时,
时,![]() 的取值范围是
的取值范围是![]() ;⑤当x1<x2<0时,y1<y2.其中结论正确的个数是( )
;⑤当x1<x2<0时,y1<y2.其中结论正确的个数是( )
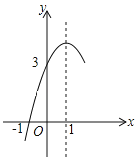
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
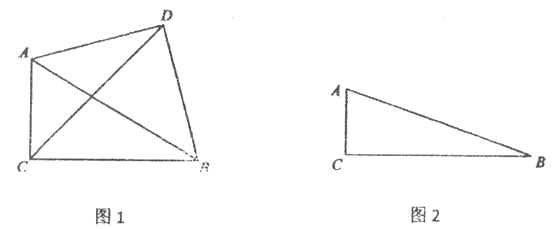
【题目】在△ABC中,∠ACB=90°,以AB为斜边作等腰直角三角形ABD,且点D与点C在直线AB的两侧,连接CD.
(1)如图1,若∠ABC=30°,则∠CAD的度数为________.
(2)已知AC=1,BC=3.
①依题意将图2补全;
②求CD的长;
(3)用等式表示线段AC,BC,CD之间的数量关系(直接写出即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列图形中,是轴对称图形的是( )
A. [Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2018/3/27/1911053122682880/1914886922772480/STEM/c8503fddf66f4b8c93035a98d8f9f214.png] B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我校4月份举办了教职工羽毛球赛,本次比赛共分三个项目:男双、女双和混双.比赛规定参赛男教师只能在男双或混双中选报一项,参赛女教师只能在女双或混双中选报一项,现将参赛人数和各项的参赛队数(两人组成一队)绘制成了如下不完整的统计图:
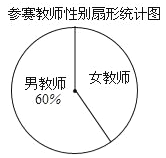
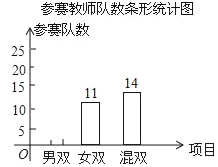
(1)本次比赛共有_____名参赛教师,并补全条形统计图;
(2)已知男双冠军分别是音乐教师和体育教师,女双冠军都是数学教师,混双冠军分别是数学男教师和美术女教师.暑假期问市教委将举办全市中小学教师羽毛球比赛,比赛规定:每所学校的参赛人数为两人,且参赛教师不得属于同一学科.所以学校决定:从三支冠军队伍中的数学教师中随机选取一人,再从其他教师中选取一人参加比赛.请用列表法或画树状图的方法求出所选两位教师恰好搭档参加混双项目的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小红两人共同计算一道整式乘法题:![]() ,小明由于抄错了第一个多项式中
,小明由于抄错了第一个多项式中![]() 的符号,即把
的符号,即把![]() 抄成
抄成![]() ,得到的结果为
,得到的结果为![]() ;小红由于漏抄了第二个多项式中x的系数,即把
;小红由于漏抄了第二个多项式中x的系数,即把![]() 抄成x,得到的结果为
抄成x,得到的结果为![]() .
.
(1)求出式子中的![]() 、
、![]() 的值
的值
(2)请你计算出这道整式乘法题的正确结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果三角形有一边上的中线长恰好等于这条边的长,那么称这个三角形为“有趣三角形”,这条中线称为“有趣中线”.已知![]() 中,
中,![]() ,一条直角边为3,如果
,一条直角边为3,如果![]() 是“有趣三角形”,那么这个三角形“有趣中线”的长等于________.
是“有趣三角形”,那么这个三角形“有趣中线”的长等于________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知同一平面内,∠AOB=90°,∠AOC=30°,
(1)画出图形并求∠COB的度数;
(2)若OD平分∠BOC,OE平分∠AOC,求∠DOE的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com