
分析 (1)原式利用乘方的意义,零指数幂,负整数指数幂法则计算即可得到结果;
(2)原式括号中两项方程并利用同分母分式的减法法则计算,乘方后利用除法法则变形,约分得到最简结果,把x的值代入计算即可求出值;
(3)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:(1)原式=(-16×1×4×$\frac{1}{64}$)×4×100=-400;
(2)原式=$\frac{(x-1)^{2}}{(x+1)^{2}}$•$\frac{x+1}{x-1}$=$\frac{x-1}{x+1}$,
当x=$\frac{1}{3}$时,原式=$\frac{\frac{1}{3}-1}{\frac{1}{3}+1}$=-$\frac{1}{2}$;
(3)去分母得:-2(x+2)+x2+x-2=x2-4,
解得:x=-2,
经检验x=-2是增根,分式方程无解.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图所示,在直角坐标系中,函数y=$\frac{k}{x}$(x>0,常数k>0)的图象经过点A(1,2),B(m,n)(m>1),过点B作y轴的垂线,垂足为C,若点C的坐标为(0,1),则△ABC的面积为1.
如图所示,在直角坐标系中,函数y=$\frac{k}{x}$(x>0,常数k>0)的图象经过点A(1,2),B(m,n)(m>1),过点B作y轴的垂线,垂足为C,若点C的坐标为(0,1),则△ABC的面积为1.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
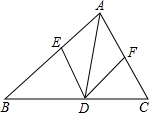 如图,在△ABC中,点D、E、F分别在边AB,BC,CA上,且DE∥CA,DF∥BA.下列结论:①四边形AEDF是平行四边形;②如果∠BAC=90°,那么四边形AEDF是矩形;③如果AD平分∠BAC,那么四边形AEDF是菱形;④如果∠BAC=90°,AD平分∠BAC,那么四边形AEDF是正方形,你认为正确的是( )
如图,在△ABC中,点D、E、F分别在边AB,BC,CA上,且DE∥CA,DF∥BA.下列结论:①四边形AEDF是平行四边形;②如果∠BAC=90°,那么四边形AEDF是矩形;③如果AD平分∠BAC,那么四边形AEDF是菱形;④如果∠BAC=90°,AD平分∠BAC,那么四边形AEDF是正方形,你认为正确的是( )| A. | ①②③④ | B. | ①②③ | C. | ①②④ | D. | ②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
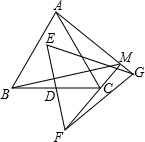 如图,△ABC,△EFG均是边长为2的等边三角形,点D是边BC、EF的中点,直线AG、FC相交于点M.当△EFG绕点D旋转时,线段BM长的最小值是( )
如图,△ABC,△EFG均是边长为2的等边三角形,点D是边BC、EF的中点,直线AG、FC相交于点M.当△EFG绕点D旋转时,线段BM长的最小值是( )| A. | 2-$\sqrt{3}$ | B. | $\sqrt{3}$+1 | C. | $\sqrt{2}$ | D. | $\sqrt{3}$-1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com