
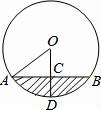
 如图表示一圆柱形输水管的横截面,阴影部分为有水部分,如果输水管的半径为5cm,水面宽AB为8cm,求(1)水的最大深度CD(2)若角AOD为50度,求阴影部分的面积.
如图表示一圆柱形输水管的横截面,阴影部分为有水部分,如果输水管的半径为5cm,水面宽AB为8cm,求(1)水的最大深度CD(2)若角AOD为50度,求阴影部分的面积. 分析 (1)根据题意可得出AO=5cm,AC=4cm,进而得出CO的长,即可得出答案.
(2)根据扇形的面积公式和三角形的面积公式解答即可.
解答 解:(1)∵输水管的半径为5cm,水面宽AB为8cm,水的最大深度为CD,
∴DO⊥AB,
∴AO=5cm,AC=4cm,
∴CO=$\sqrt{{5}^{2}-{4}^{2}}$=3(cm),
∴水的最大深度CD为:2cm;
(2)∵∠AOD=50°,
∴${S}_{扇AOD}=\frac{nπ{r}^{2}}{360°}=\frac{50°π•{5}^{2}}{360°}=\frac{125π}{36}$,
∵OC=2,
∴${S}_{△ACO}=\frac{1}{2}×4×3=6$,
∴阴影部分的面积=$2(\frac{125π}{36}-6)=\frac{125π}{18}-12≈9.8$cm2.
点评 本题考查的是垂径定理的应用及勾股定理,根据构造出直角三角形是解答此题的关键.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
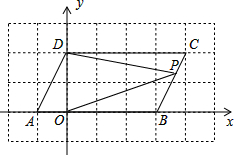 在平面直角坐标系中,点A,B的坐标分别为A(a,0),B(b,0),且a,b满足|a+b-2|+$\sqrt{2a-b+5}$=0,现同时将点A,B分别向右平移1个单位,再向上平移2个单位,分别得到点A,B的对应点为C,D.
在平面直角坐标系中,点A,B的坐标分别为A(a,0),B(b,0),且a,b满足|a+b-2|+$\sqrt{2a-b+5}$=0,现同时将点A,B分别向右平移1个单位,再向上平移2个单位,分别得到点A,B的对应点为C,D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
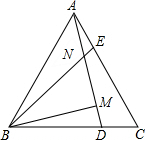 已知:如图:等边△ABC,D、E分别是BC、AC上的点,AD、BE交于N,BM⊥AD于M,若AE=CD,求证:
已知:如图:等边△ABC,D、E分别是BC、AC上的点,AD、BE交于N,BM⊥AD于M,若AE=CD,求证:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com