Question

半径为3和2的两圆，已知这两圆连心线的延长线与一条外公切线的夹角为30°，则两圆的位置关系是________．

Answer 1

相交
分析：此题要能够把要求的角转化到直角三角形中，根据解直角三角形的知识求解．
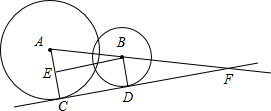
解答：解：如图，由已知条件得AC=3，BD=2，
作BE⊥AC于点E，
∴AE=AC-BD=3-2=1
∵这两圆连心线的延长线与一条外公切线的夹角为30°，
∴∠ABE=30°，
∴AB=2AE=2
∴1＜2＜5
∴两圆相交，
故答案为：相交．
点评：本题考查了圆与圆的位置关系，注意常见的辅助线：出现外公切线时，通常情况下应连接两圆圆心和切点，过小圆圆心向大圆半径引垂线，可得到一矩形，和一直角三角形．