
【题目】如图,在△ABC中,AB=3,AC=4,BC=5,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值为 . 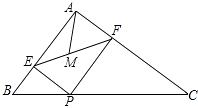
【答案】![]()
【解析】解:∵AB=3,AC=4,BC=5, ∴∠EAF=90°,
∵PE⊥AB于E,PF⊥AC于F,
∴四边形AEPF是矩形,
∴EF,AP互相平分.且EF=AP,
∴EF,AP的交点就是M点.
∵当AP的值最小时,AM的值就最小,
∴当AP⊥BC时,AP的值最小,即AM的值最小.
∵ ![]() AP.BC=
AP.BC= ![]() AB.AC,
AB.AC,
∴AP.BC=AB.AC.
∵AB=3,AC=4,BC=5,
∴5AP=3×4,
∴AP= ![]() ,
,
∴AM= ![]() ;
;
故答案为: ![]() .
.
先根据矩形的判定得出AEPF是矩形,再根据矩形的性质得出EF,AP互相平分,且EF=AP,再根据垂线段最短的性质就可以得出AP⊥BC时,AP的值最小,即AM的值最小,根据面积关系建立等式求出其解即可.


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,当过O点画不重合的2条射线时,共组成1个角;当过O点画不重合的3条射线时,共组成3个角;当过O点画不重合的4条射线时,共组成6个角;….根据以上规律,当过O点画不重合的10条射线时,共组成( )个角.
A.28
B.36
C.45
D.55
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,真命题是( ) .
A. 对角线相等的四边形是矩形;
B. 对角线互相垂直的四边形是菱形;
C. 对角线互相平分的四边形是平行四边形;
D. 对角线互相垂直平分的四边形是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=8,点E,F分别在AB,AD上,且AE=AF,过点E作EG∥AD交CD于点G,过点F作FH∥AB交BC于点H,EG与FH交于点O.当四边形AEOF与四边形CGOH的周长之差为12时,AE的值为( ) 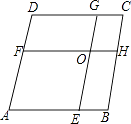
A.6.5
B.6
C.5.5
D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明家的住房平面图呈长方形,被分割成3个正方形和2个长方形后仍是中心对称图形.若只知道原住房平面图长方形的周长,则分割后不用测量就能知道周长的图形的标号为( )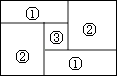
A.①②
B.②③
C.①③
D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平行四边形ABCD中,AB=2AD.
(1)作AE平分∠BAD交DC于E(尺规作图,保留作图痕迹);
(2)在(1)的条件下,连接BE,判定△ABE的形状(不要求证明).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,M、N分别是AD、BC的中点,P、Q分别是BM、DN的中点. 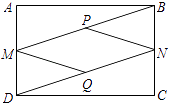
(1)求证:△MBA≌△NDC;
(2)求证:四边形MPNQ是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,AB=AC,∠A=36°.
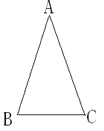
(1)作∠ABC的平分线BD,交AC于点D(用尺规作图法,保留作图痕迹,不要求写作法);
(2)在(1)条件下,比较线段DA与BC的大小关系(不要求证明).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com