
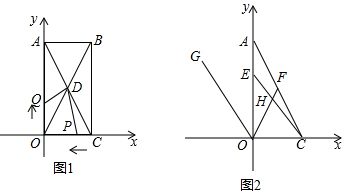
���� ��1�����ݾ���ֵ������ƽ�����ķǸ��ԣ����a��b��ֵ���ɣ�
��2���ٵ�0��t��2ʱ���ڵ�2��t��3ʱ���۵�3��t��5ʱ���ٸ���S��ODP=S��ODQ���г�����t�ķ��̣����t��ֵ���ɣ�
��3����H����AC��ƽ���ߣ���x����P�����ж�OG��AC���ٸ��ݽǵĺͲ��ϵ�Լ�ƽ���ߵ����ʣ��ó���PHO=��GOF=��1+��2����OHC=��OHP+��PHC=��GOF+��4=��1+��2+��4��������$\frac{��OHC+��ACE}{��OEC}$���м��㼴�ɣ�
��� 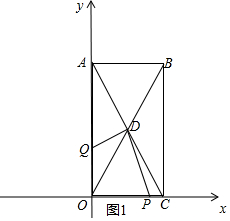 �⣺��1����$\sqrt{a-2b}$+|b-2|=0��
�⣺��1����$\sqrt{a-2b}$+|b-2|=0��
��a-2b=0��b-2=0��
���a=4��b=2��
��A��0��4����C��2��0����
��AB��x�ᣬBC��y�ᣬ
��B��2��4����
��2����������֪��P���C���˶���O��ʱ��Ϊ2�룬Q���O���˶���A��ʱ��Ϊ2�룬
�ٵ�0��t��2ʱ����Q���߶�AO�ϣ�
�� CP=t��OP=2-t��OQ=2t��AQ=4-2t��
��S��DOP=$\frac{1}{2}$OP•yD=$\frac{1}{2}$��2-t����2=2-t��
��S��ODP=S��ODQ��
��2-t=t��
��t=1��
�ڵ�2��t��3ʱ����Q���߶�AB�ϣ���CP=t��OP=t-2��QB=6-2t��
S��DOP=$\frac{1}{2}$OP•yD=$\frac{1}{2}$��t-2����2=t-2��
S��DOP=S��OBQ-S��DBQ=$\frac{1}{2}$QB•AO-$\frac{1}{2}$QB��yB-yD��=$\frac{1}{2}$����6-2t����4-$\frac{1}{2}��$��6-2t����4-2��=6-2t��
��S��DOQ=S��ODQ��
��t-2=6-2t��
��t=$\frac{8}{3}$��
�۵�3��t��5ʱ����Q���߶�BC�ϣ�CP=t��OP=t-2��QB=2t-6��
S��DOP=$\frac{1}{2}$OP•yD=$\frac{1}{2}$��t-2����=t-2��
S��DOQ=S��OBQ-S��DBQ=$\frac{1}{2}$QB•OC-$\frac{1}{2}$QB��xB-xD��=$\frac{1}{2}$����2t-6��-$\frac{1}{2}$��6-2t����2-1��=t-3��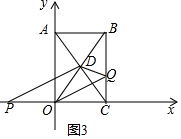
��S��ODP=S��ODQ��
��t-2=t-3���⣬
������²�����������t��
�൱t=1��t=$\frac{8}{3}$ʱ��S��ODP=S��ODQ��
��3��$\frac{��OHC+��ACE}{��OEC}$��ֵ���䣬��ֵΪ2��
�ߡ�2+��3=90�㣬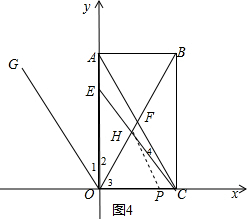
�֡ߡ�1=��2����3=��FCO��
���GOC+��ACO=180�㣬
��OG��AC��
���1=��CAO��
���OEC=��CAO+��4=��1+��4��
��ͼ����H����AC��ƽ���ߣ���x����P�����4=��PHC��PH��OG��
���PHO=��GOF=��1+��2��
���OHC=��OHP+��PHC=��GOF+��4=��1+��2+��4��
��$\frac{��OHC+��ACE}{��OEC}$=$\frac{��1+��2+��4+��4}{��1+��4}$=$\frac{2����1+��4��}{��1+��4}$=2��
���� ������Ҫ������������ͼ�����ʣ��������Ĺؼ�ֵ�������߹���ƽ���ߣ�����ʱע�⣺����һ�����ľ���ֵ���ǷǸ���������ƽ�������зǸ��ԣ��Ǹ���֮�͵���0ʱ���������0��


 �ŵ������ϵ�д�
�ŵ������ϵ�д� 53������ϵ�д�
53������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����A������Ϊ��-3��0������B��ֱ��y=-x���˶�������AB�����߶�AB���ʱ����B����Ϊ��-1.5��1.5����
��ͼ����A������Ϊ��-3��0������B��ֱ��y=-x���˶�������AB�����߶�AB���ʱ����B����Ϊ��-1.5��1.5�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x=-3 | B�� | x1=0��x2=-3 | C�� | x=3 | D�� | x1=0��x2=3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
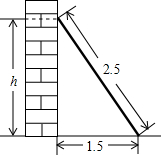 ��ͼ����2.5m�����ӿ���ǽ�ϣ����ӵĵײ���ǽ�ĵ�1.5m�������ӵĶ��������ľ���Ϊ2m��
��ͼ����2.5m�����ӿ���ǽ�ϣ����ӵĵײ���ǽ�ĵ�1.5m�������ӵĶ��������ľ���Ϊ2m���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{3}$ | B�� | $\frac{1}{8}$ | C�� | $\frac{4}{15}$ | D�� | $\frac{4}{11}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com