
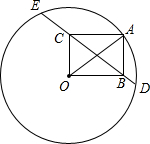
 如图,⊙O的半径为20,A是⊙O上一点.以OA为对角线作矩形OBAC,且OC=12.延长BC,与⊙O分别交于D,E两点,则CE-BD的值等于
如图,⊙O的半径为20,A是⊙O上一点.以OA为对角线作矩形OBAC,且OC=12.延长BC,与⊙O分别交于D,E两点,则CE-BD的值等于 解:如图,设DE的中点为M,连接OM,则OM⊥DE.
解:如图,设DE的中点为M,连接OM,则OM⊥DE.| OA2-AB2 |
| 202-122 |
| OB•OC |
| BC |
| 16×12 |
| 20 |
| 48 |
| 5 |
| OC2-OM2 |
122-(
|
| 36 |
| 5 |
| 36 |
| 5 |
| 64 |
| 5 |
| 64 |
| 5 |
| 36 |
| 5 |
| 28 |
| 5 |
| 28 |
| 5 |


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
 如图,在Rt△ABC中,∠BAC=90°,∠B=60°,BC=16cm,AD是斜边BC上的高,垂足为D,BE=1cm.点M从点B出发沿BC方向以1cm/s的速度运动,点N从点E出发,与点M同时同方向以相同的速度运动,以MN为边在BC的上方作正方形MNGH.点M到达点D时停止运动,点N到达点C时停止运动.设运动时间为t(s).
如图,在Rt△ABC中,∠BAC=90°,∠B=60°,BC=16cm,AD是斜边BC上的高,垂足为D,BE=1cm.点M从点B出发沿BC方向以1cm/s的速度运动,点N从点E出发,与点M同时同方向以相同的速度运动,以MN为边在BC的上方作正方形MNGH.点M到达点D时停止运动,点N到达点C时停止运动.设运动时间为t(s).查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,点M是△ABC内-点,过点M分别作直线平行于△ABC的各边,所形成的三个小三角形△1、△2、△3(图中阴影部分)的面积分别是1,4,9.则△ABC的面积是
如图,点M是△ABC内-点,过点M分别作直线平行于△ABC的各边,所形成的三个小三角形△1、△2、△3(图中阴影部分)的面积分别是1,4,9.则△ABC的面积是查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 在全民健身环城越野赛中,甲乙两选手的行程y(千米)随时间(时)变化的图象(全程)如图所示.则根据图象,起跑后1小时内,跑在前面的是
在全民健身环城越野赛中,甲乙两选手的行程y(千米)随时间(时)变化的图象(全程)如图所示.则根据图象,起跑后1小时内,跑在前面的是查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com