
【题目】某商店今年1月份的销售额是2万元,3月份的销售额是3.38万元.
(1)求从1月份到3月份,该商店销售额平均每月的增长率;
(2)如果该商店4月份销售额增长率保持不变,销售额能否达到4.5万元,若不能,请说明理由.
【答案】(1)从1月份到3月份,该店销售额平均每月的增长率为30%;(2)不能.理由见解析.
【解析】试题分析:
(1) 设每月增长率为x,据题意可知:三月份销售额为2(1+x)2万元,依此等量关系列出方程,求解即可.
(2) 根据该商店4月份销售额增长率保持不变,计算出4月份销售额,和4.5万元进行比较即可.
试题解析:
解:⑴ 设该店销售额平均每月的增长率为x,
则二月份销售额为![]() 万元,三月份销售额为
万元,三月份销售额为![]() 万元,
万元,
由题意可得:![]() ,
,
解得:x1=0.3=30%,x2=﹣2.3(不合题意舍去),
答:从1月份到3月份,该店销售额平均每月的增长率为30%;
⑵ 不能.理由如下:
∵ 该商店4月份销售额增长率保持不变
∴ 四月份销售额为![]() 万元
万元
当x=0.3时,
![]()


科目:初中数学 来源: 题型:
【题目】风电已成为我国继煤电、水电之后的第三大电源,风电机组主要由塔杆和叶片组成(如图1),图2是从图1引出的平面图.假设你站在A处测得塔杆顶端C的仰角是55°,沿HA方向水平前进43米到达山底G处,在山顶B处发现正好一叶片到达最高位置,此时测得叶片的顶端D(D、C、H在同一直线上)的仰角是45°.已知叶片的长度为35米(塔杆与叶片连接处的长度忽略不计),山高BG为10米,BG⊥HG,CH⊥AH,求塔杆CH的高.(参考数据:tan55°≈1.4,tan35°≈0.7,sin55°≈0.8,sin35°≈0.6)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在探究一次函数![]() 的图像性质时我们有如下发现:
的图像性质时我们有如下发现:
①系数![]() 决定了函数图像的坡度,
决定了函数图像的坡度,![]() 越大则图像坡度越大(越靠近
越大则图像坡度越大(越靠近![]() 轴),
轴),![]() 越小则图像坡度越小(越靠近
越小则图像坡度越小(越靠近![]() 轴);
轴);
②常数项![]() 决定了图像与
决定了图像与![]() 轴的交点,即函数图像与
轴的交点,即函数图像与![]() 轴交点坐标始终为
轴交点坐标始终为![]() .
.
基于以上发现,我们得出结论:如果两个一次函数的![]() 值相同,那么两个一次函数的图像平行.反之,如果两直线平行,则两条直线所对应的函数表达式的
值相同,那么两个一次函数的图像平行.反之,如果两直线平行,则两条直线所对应的函数表达式的![]() 值一定相等:把函数图像沿
值一定相等:把函数图像沿![]() 轴向上(或向下) 平移
轴向上(或向下) 平移![]() 个单位, 系数
个单位, 系数![]() 保持不变, 常数
保持不变, 常数![]() 变为
变为![]() (或
(或![]() ).如:函数
).如:函数![]() 和
和![]() 的图像互相平行:函数
的图像互相平行:函数![]() 的图像向上平移2个单位后所得函数表达式为
的图像向上平移2个单位后所得函数表达式为![]() .
.
据此回答下列问题:
(1) 把函数![]() 的图像向上平移4个单位后所得函数的表达式为____;
的图像向上平移4个单位后所得函数的表达式为____;
(2)把函数![]() 的图像向 (上或下)平移 个单位可得到函数
的图像向 (上或下)平移 个单位可得到函数![]() 的图像;
的图像;
(3)若直线![]() 经过点
经过点![]() 且与直线
且与直线![]() 平行,求出直线
平行,求出直线![]() 的表达式.
的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上有A、B两点.
![]()
(1)分别写出A、B两点表示的数: 、 ;
(2)若点C表示﹣0.5,把点C表示在如图所示的数轴上;
(3)将点B向左移动3个单位长度,得到点D,点A、B、C、D所表示的四个数用“<”连接的结果: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F,连接CF.
(1)求证:AF=BD.
(2)求证:四边形ADCF是菱形.

查看答案和解析>>
科目:初中数学 来源: 题型:
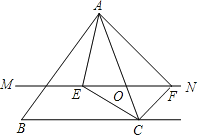
【题目】如图,在△ABC中,点O是AC边上(端点除外)的一个动点,过点O作直线MN∥BC.设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F,连接AE、AF.那么当点O运动到何处时,四边形AECF是矩形?并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
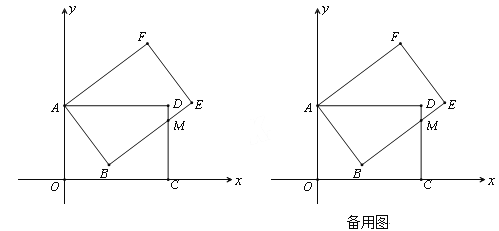
【题目】矩形AOCD绕顶点A(0,5)逆时针方向旋转,当旋转到如图所示的位置时,边BE交边CD于M,且ME=2,CM=4.
(1)求AD的长;
(2)求经过A、B、D三点的抛物线的解析式;
(3)在直线AM下方,(2)中的抛物线上是否存在点P,使S△PAM =![]() ?若存在,求出P点坐标;若不存在,请说明理由.
?若存在,求出P点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,|a|表示a到原点的距离,这是绝对值的几何意义.进一步地,数轴上两个点A、B,分别用a、b表示,那么AB=|a-b|.(思考一下,为什么?),利用此结论,回答以下问题:
(1)数轴上表示2和5的两点之间的距离是_____.数轴上表示-2和-5的两点之间的距离___.数轴上表示1和-3的两点之间的距离是_____;
(2)数轴上表示x和-1的两点A、B之间的距离是___________;
如果|AB|=2,x的值为_____;
(3)说出|x+1|+|x+2|表示几何的意义_,该代数式的最小值是:_____;
(4)求|x-1|+|x-2|+|x-3|+...+|x-2019|的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com