
【题目】如图17-Z-12所示,等腰三角形ABC的底边长为8 cm,腰长为5 cm,一动点P在底边上从点B向点C以0.25 cm/s的速度移动,请你探究:当点P运动几秒时,点P与顶点A的连线AP与腰垂直?

图17-Z-12
【答案】当点P运动7 s或25 s时,点P与顶点A的连线AP与腰垂直
【解析】试题分析:分类讨论,AP分别与两个腰垂直,利用勾股定理计算时间.
应分两种情况:
(1)设当点P运动t(0≤t≤32)s时,AP与腰AC垂直,过点A作AD⊥BC,垂足为D,如图①所示.因为△ABC为等腰三角形,所以D为BC的中点,则BD=CD=4 cm,根据勾股定理得AD=3 cm.在Rt△ACP中,AP2=CP2-AC2=(8-0.25t)2-52,在Rt△ADP中,AP2=AD2+DP2=32+(4-0.25t)2,所以(8-0.25t)2-52=32+(4-0.25t)2,解得t=7.因此当23点P运动7 s时,AP与腰AC垂直.

(2)设当点P运动t(0≤t≤32)s时,AP与腰AB垂直,过点A作AD⊥BC,垂足为D,如图②所示.因为△ABC为等腰三角形,所以D为BC的中点,则BD=CD=4 cm,根据勾股定理得AD=3 cm.在Rt△ABP中,AP2=BP2-AB2=(0.25t)2-52,在Rt△ADP中,AP2=AD2+DP2=32+(0.25t-4)2,所以(0.25t)2-52=32+(0.25t-4)2,解得t=25.因此当点P运动25 s时,AP与腰AB垂直.
综上,当点P运动7 s或25 s时,点P与顶点A的连线AP与腰垂直


科目:初中数学 来源: 题型:
【题目】如图,已知E是正方形ABCD的边CD外的一点,△DCE为等边三角形,BE交对角线AC于F .
(1)求∠AFD的度数;
(2)求证:AF = EF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某食品厂从生产的袋装食品中抽出样品20袋,检测每袋的质量是否符合标准,超过或不足的部分分别用正、负数来表示,记录如下表:
与标准质量的差值 |
|
| 0 | 1 | 3 | 6 |
袋 数 | 1 | 4 | 3 | 4 | 5 | 3 |
(1)这批样品的平均质量比标准质量多还是少?多或少几克?
(2)若每袋标准质量为450克,则抽样检测的总质量是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图 (1),已知△ABC是等边三角形,以BC为直径的⊙O交AB、AC于D、E.求证:
(1)△DOE是等边三角形.
(2)如图(2),若∠A=60°,AB≠AC , 则(1)中结论是否成立?如果成立,请给出证明;如果不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在足球比赛中,甲、乙两名队员互相配合向对方球门MN进攻,当甲带球冲到A点时,乙已跟随冲到B点,如图24-1-4-12.此时,甲自己直接射门好,还是迅速将球传给乙,让乙射门好?
查看答案和解析>>
科目:初中数学 来源: 题型:
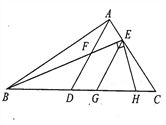
【题目】如图,在△ABC中,点D在BC 上,点E 在AC 上,AD交BE于F. 已知EG∥AD交BC于G, EH⊥BE交BC于H,∠HEG = 50°.
(1)求∠BFD的度数.
(2)若∠BAD = ∠EBC,∠C = 41°,求∠BAC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B、E分别在直线AC和DF上,若∠AGB=∠EHF,∠C=∠D,可以证明∠A=∠F.请完成下面证明过程中的各项“填空”.

证明:∵∠AGB=∠EHF(理由: )
∠AGB= (对顶角相等)
∴∠EHF=∠DGF,∴DB∥EC(理由: )
∴ =∠DBA(两直线平行,同位角相等)
又∵∠C=∠D,∴∠DBA=∠D,
∴DF∥ (内错角相等,两直线平行)
∴∠A=∠F(理由: ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.
(1)求证:CE=CF;
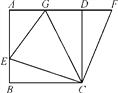
(2)若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线y=2x-2与x轴交于点A,与y轴交于点B.
(1)求点A,B的坐标;
(2)点C在x轴上,且S△ABC=3S△AOB,直接写出点C的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com