
【题目】直线y=2x-2与x轴交于点A,与y轴交于点B.
(1)求点A,B的坐标;
(2)点C在x轴上,且S△ABC=3S△AOB,直接写出点C的坐标.

【答案】(1)A(1,0),B(0,-2);(2)(4,0)或(-2,0).
【解析】【试题分析】(1)直接代入函数解析式,当x=0时,求出纵坐标;当y=0时,求出横坐标,即可表示出A、B两点的坐标;
(2)根据S△ABC=3S△AOB,这两个三角形的高相等,只需AC=3OA即可.
【试题解析】
(1)令y=2x-2中y=0,则2x-2=0,解得x=1,∴A(1,0).令y=2x-2中x=0,则y=-2,∴B(0,-2).
(2)根据题意画出图形,如图所示.

设点C的坐标为(m,0),
∵S△ABC=3S△AOB,
∴|m-1|=3,解得m=4或m=-2,
即点C的坐标为(4,0)或(-2,0).


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图17-Z-12所示,等腰三角形ABC的底边长为8 cm,腰长为5 cm,一动点P在底边上从点B向点C以0.25 cm/s的速度移动,请你探究:当点P运动几秒时,点P与顶点A的连线AP与腰垂直?

图17-Z-12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD是平行四边形,对角线AC、BD交于点O,E是BC的中点,以下说法错误的是( )

A. OE=![]() DC B. OA=OC C. ∠BOE=∠OBA D. ∠OBE=∠OCE
DC B. OA=OC C. ∠BOE=∠OBA D. ∠OBE=∠OCE
查看答案和解析>>
科目:初中数学 来源: 题型:
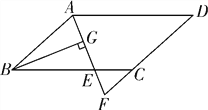
【题目】如图,在平行四边形ABCD中,AB=6,AD=10,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G,AG=2.5,则△CEF的周长为
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,线段AB和射线BM交于点B.
(1)利用尺规完成以下作图,并保留作图痕迹(不写作法)
①在射线BM上作一点C,使AC=AB;
②作∠ABM 的角平分线交AC于D点;
③在射线CM上作一点E,使CE=CD,连接DE.

(2)在(1)所作的图形中,猜想线段BD与DE的数量关系,并证明之.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子中,共有“一红二白”三个球,它们除颜色外其余都相同.
(1)从盒子中摸出1个球,是白球的概率是多少?
(2)从盒子中摸出1个球,不放回再摸出1个球,请用画树状图或列表的方式表示出所有可能的结果,并求出摸出的恰好是“一红一白”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某人共收集邮票若干张,其中![]() 是2000年以前的国内外发行的邮票,
是2000年以前的国内外发行的邮票,![]() 是2001年国内发行的,
是2001年国内发行的,![]() 是2002年国内发行的,此外尚有不足100张的国外邮票.求该人共有多少张邮票.
是2002年国内发行的,此外尚有不足100张的国外邮票.求该人共有多少张邮票.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据我国古代《周髀算经》记载,大约公元1120年,商高曾对周公说过一段话,其意思是将一根直尺折成一个直角,两端连接得一个直角三角形,如果勾是三,股是四,那么弦就等于五,后人概括为“勾三股四弦五”。
(1)观察:3,4,5; 5,12,13; 7,24,25……发现这些勾股数的勾都是奇数,且从3起就没有间断过。计算![]() ,
, ![]() 与
与![]() ,
, ![]() 并根据发现的规律,分别写出能表示7,24,25的股和弦的算式;
并根据发现的规律,分别写出能表示7,24,25的股和弦的算式;
(2)根据(1)的规律,用n(n为奇数且n≥3)的代数式来表示所有这些勾股数的勾、股、弦,合理猜想它们之间的两种相等关系并对其一种猜想加以说明。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com