
【题目】据我国古代《周髀算经》记载,大约公元1120年,商高曾对周公说过一段话,其意思是将一根直尺折成一个直角,两端连接得一个直角三角形,如果勾是三,股是四,那么弦就等于五,后人概括为“勾三股四弦五”。
(1)观察:3,4,5; 5,12,13; 7,24,25……发现这些勾股数的勾都是奇数,且从3起就没有间断过。计算![]() ,
, ![]() 与
与![]() ,
, ![]() 并根据发现的规律,分别写出能表示7,24,25的股和弦的算式;
并根据发现的规律,分别写出能表示7,24,25的股和弦的算式;
(2)根据(1)的规律,用n(n为奇数且n≥3)的代数式来表示所有这些勾股数的勾、股、弦,合理猜想它们之间的两种相等关系并对其一种猜想加以说明。
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:初中数学 来源: 题型:
【题目】直线y=2x-2与x轴交于点A,与y轴交于点B.
(1)求点A,B的坐标;
(2)点C在x轴上,且S△ABC=3S△AOB,直接写出点C的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,A(1,0)、点B在y轴上,将三角形OAB沿x轴负方向平移,平移后的图形为三角形DEC,且点C的坐标为(﹣3,2).
(1)直接写出点E的坐标 ;
(2)在四边形ABCD中,点P从点B出发,沿“BC→CD”移动.若点P的速度为每秒1个单位长度,运动时间为t秒,回答下列问题:
①当t= 秒时,点P的横坐标与纵坐标互为相反数;
②求点P在运动过程中的坐标,(用含t的式子表示,写出过程);
③当3秒<t<5秒时,设∠CBP=x°,∠PAD=y°,∠BPA=z°,试问 x,y,z之间的数量关系能否确定?若能,请用含x,y的式子表示z,写出过程;若不能,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣(x﹣1)2+4与x轴交于点A,B(点A在点B的左侧),与y轴交于点C,CD∥x轴交抛物线另一点D,连结AC,DE∥AC交边CB于点E. 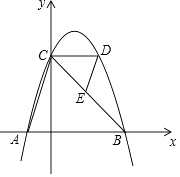
(1)求A,B两点的坐标;
(2)求△CDE与△BAC的面积之比.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:(1)![]() +(
+(![]() -
-![]() )÷(-
)÷(-![]() ); (2)-1-(1-
); (2)-1-(1-![]() )÷3×|3-9|;
)÷3×|3-9|;
(3)1![]() +(2.4×
+(2.4×![]() -
-![]() ×
×![]() )÷2
)÷2![]() ; (4)(-3-1
; (4)(-3-1![]() )÷[3
)÷[3![]() ÷(2-3
÷(2-3![]() )×1
)×1![]() ].
].
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD中,BD⊥AD,∠A=45°,E、F分别是AB,CD上的点,且BE=DF,连接EF交BD于O. 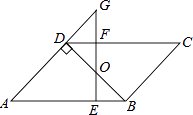
(1)求证:BO=DO;
(2)若EF⊥AB,延长EF交AD的延长线于G,当FG=1时,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是将菱形ABCD以点O为中心按顺时针方向分别旋转90°,180°,270°后形成的图形。若![]() ,AB=2,则图中阴影部分的面积为( )
,AB=2,则图中阴影部分的面积为( )

A. 12-4![]() B. 5 C. 12-4
B. 5 C. 12-4![]() D. 6
D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,将矩形AOCD沿直线AE折叠(点E在边DC上),折叠后顶点D恰好落在边OC上的点F处,若点D的坐标为(10,8),求点E的坐标
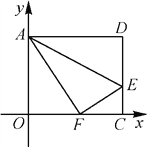
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com