
【题目】如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.
(1)求证:CE=CF;
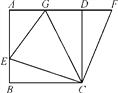
(2)若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?
【答案】(1)证明见解析(2)GE=BE+GD成立
【解析】试题分析:(1)由DF=BE,四边形ABCD为正方形可证△CEB≌△CFD,从而证出CE=CF;
(2)由(1)得CE=CF,∠BCE+∠ECD=∠DCF+∠ECD,即∠ECF=∠BCD=90°,又∠GCE=45°,所以可得∠GCE=∠GCF,故可证得△ECG≌△FCG,即EG=FG=GD+DF.又因为DF=BE,所以可证出GE=BE+GD成立.
试题解析:(1)∵在正方形ABCD中,BC=CD,∠B=∠CDF,BE=DF,
∴△CBE≌△CDF(SAS)
∴CE=CF.
(2)GE=BE+GD成立.
理由:由(1),得△CBE≌△CDF,
∴∠BCE=∠DCF,
∴∠BCE+∠ECD=∠DCF+∠ECD,即∠BCD=∠ECF=90°,
又∵∠GCE=45°,
∴∠GCF=∠GCE=45°,
∵CE=CF,∠GCE=∠GCF,GC=GC,
∴△ECG≌△FCG(SAS),
∴GE=GF,
∴GE=DF+GD=BE+GD.


科目:初中数学 来源: 题型:
【题目】甲、乙两家超市以相同的价格出售同样的商品,为了吸引顾客,各自推出不同的优惠方案:在甲超市累计购买商品超出300元之后,超出部分按原价8折优惠;在乙超市累计购买商品超出200元之后,超出部分按原价8.5折优惠.设顾客预计累计购物![]() 元(
元(![]() ).
).
(1)请用含![]() 的代数式分别表示顾客在两家超市购物所付的费用;
的代数式分别表示顾客在两家超市购物所付的费用;
(2)李明准备购买500元的商品,你认为他应该去哪家超市?请说明理由;
(3)计算一下,李明购买多少元的商品时,到两家超市购物所付的费用一样?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图17-Z-12所示,等腰三角形ABC的底边长为8 cm,腰长为5 cm,一动点P在底边上从点B向点C以0.25 cm/s的速度移动,请你探究:当点P运动几秒时,点P与顶点A的连线AP与腰垂直?

图17-Z-12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角梯形ABCD中,AD∥BC,∠C=90°,AD=5,BC=9,以A为中心将腰AB顺时针旋转90°至AE,连接DE,则△ADE的面积等于( )
A.10
B.11
C.12
D.13
查看答案和解析>>
科目:初中数学 来源: 题型:
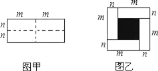
【题目】已知图甲是一个长为2m,宽为2n的长方形,沿图甲中虚线用剪刀均匀分成四小块长方形,然后按图乙的形状拼成一个正方形.
(1)图乙中阴影部分正方形的边长为 (用含字母m,n的整式表示).
(2)请用两种不同的方法求图乙中阴影部分的面积.
方法一: ;
方法二: .
(3)观察图乙,并结合(2)中的结论,你能写出下列三个整式:(m+n)2,(m﹣n)2,mn之间的等量关系吗?
(4)根据(3)题中的等量关系,解决如下问题:若a+b=9,ab=5,求(a﹣b)2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
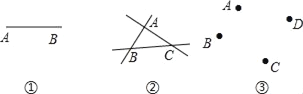
【题目】观察图①,由点A和点B可确定 条直线;
观察图②,由不在同一直线上的三点A、B和C最多能确定 条直线;
(1)动手画一画图③中经过A、B、C、D四点的所有直线,最多共可作 条直线;
(2)在同一平面内任三点不在同一直线的五个点最多能确定 条直线、n个点(n≥2)最多能确定 条直线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD是平行四边形,对角线AC、BD交于点O,E是BC的中点,以下说法错误的是( )

A. OE=![]() DC B. OA=OC C. ∠BOE=∠OBA D. ∠OBE=∠OCE
DC B. OA=OC C. ∠BOE=∠OBA D. ∠OBE=∠OCE
查看答案和解析>>
科目:初中数学 来源: 题型:
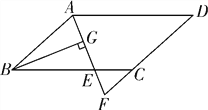
【题目】如图,在平行四边形ABCD中,AB=6,AD=10,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G,AG=2.5,则△CEF的周长为
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某人共收集邮票若干张,其中![]() 是2000年以前的国内外发行的邮票,
是2000年以前的国内外发行的邮票,![]() 是2001年国内发行的,
是2001年国内发行的,![]() 是2002年国内发行的,此外尚有不足100张的国外邮票.求该人共有多少张邮票.
是2002年国内发行的,此外尚有不足100张的国外邮票.求该人共有多少张邮票.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com