
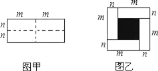
【题目】已知图甲是一个长为2m,宽为2n的长方形,沿图甲中虚线用剪刀均匀分成四小块长方形,然后按图乙的形状拼成一个正方形.
(1)图乙中阴影部分正方形的边长为 (用含字母m,n的整式表示).
(2)请用两种不同的方法求图乙中阴影部分的面积.
方法一: ;
方法二: .
(3)观察图乙,并结合(2)中的结论,你能写出下列三个整式:(m+n)2,(m﹣n)2,mn之间的等量关系吗?
(4)根据(3)题中的等量关系,解决如下问题:若a+b=9,ab=5,求(a﹣b)2的值.
【答案】(1)m-n;(2)方法一:(m+n)﹣4mn ;方法二:(m-n);
(3)(m+n)2﹣4mn=(m﹣n)2;(4)61.
【解析】
平均分成后,每个小长方形的长为m,宽为n.
(1)正方形的边长=小长方形的长-宽;
(2)第一种方法为:大正方形面积-4个小长方形面积,第二种表示方法为:阴影部分为小正方形的面积;
(3)利用(2)的结论,可得(m+n)2-4mn=(m-n)2;
(4)根据(3)的结论,可得(a-b)2=(a+b)2-4ab,代入已知值可求解.
解:(1)图乙中阴影部分正方形的边长为m﹣n;
(2)方法一:(m+n)2﹣4mn;
方法二:(m﹣n)2;
(3)由(2)可得:(m+n)2﹣4mn=(m﹣n)2;
(4)由(3)可得:
(a﹣b)2=(a+b)2﹣4ab,
∵a+b=9,ab=5,
∴(a﹣b)2=81﹣20=61.
故答案为:m﹣n;(m+n)2﹣4mn;(m﹣n)2.


 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:初中数学 来源: 题型:
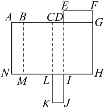
【题目】如图所示是长方体的平面展开图.
(1)将平面展开图折叠成一个长方体,与字母N重合的点有哪几个?
(2)若AG=CK=14 cm,FG=2 cm,LK=5 cm,则该长方体的表面积和体积分别是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在足球比赛中,甲、乙两名队员互相配合向对方球门MN进攻,当甲带球冲到A点时,乙已跟随冲到B点,如图24-1-4-12.此时,甲自己直接射门好,还是迅速将球传给乙,让乙射门好?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B、E分别在直线AC和DF上,若∠AGB=∠EHF,∠C=∠D,可以证明∠A=∠F.请完成下面证明过程中的各项“填空”.

证明:∵∠AGB=∠EHF(理由: )
∠AGB= (对顶角相等)
∴∠EHF=∠DGF,∴DB∥EC(理由: )
∴ =∠DBA(两直线平行,同位角相等)
又∵∠C=∠D,∴∠DBA=∠D,
∴DF∥ (内错角相等,两直线平行)
∴∠A=∠F(理由: ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上有A、B、C、D四个点,且线段AB=4,CD=6,已知A表示的数是﹣10,C表示的数是8,若线段AB以每秒6个单位长度的速度,线段CD以每秒2个单位长度的速度在数轴上运动(A在B左侧,C在D左侧)
(1)B,D两点所表示的数分别是 、 ;
(2)若线段AB向右运动,同时线段CD向左运动,经过多少秒时,BC=2;
(3)若线段AB、CD同时向右运动,同时点P从原点出发以每秒1个单位长度的速度向右运动,经过多少秒时,点P到点A,C的距离相等?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.
(1)求证:CE=CF;
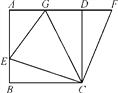
(2)若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C在线段AB上,AC=8 cm,CB=6 cm,点M、N分别是AC、BC的中点.
(1)求线段MN的长;
(2)若C为线段AB上任一点,满足AC+CB=a cm,其它条件不变,你能猜想MN的长度吗?并说明理由;
(3)若C在线段AB的延长线上,且满足AC﹣BC=bcm,M、N分别为AC、BC的中点,你能猜想MN的长度吗?请画出图形,写出你的结论,并说明理由;
(4)你能用一句简洁的话,描述你发现的结论吗?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列哪组条件能够判别四边形ABCD是平行四边形?( )

A. AB∥CD,AD=BC B. AB=CD,AD=BC
C. ∠A=∠B,∠C=∠D D. AB=AD,CB=CD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为了测量某建筑物CE的高度,先在地面上用测角仪自A处测得建筑物顶部的仰角是45°,然后在水平地面上向建筑物前进了20m,此时自B处测得建筑物顶部的仰角是60°,已知测角仪的高度是1m,请你计算出该建筑物的高度(取 ![]() ≈1.732,结果精确到1m).
≈1.732,结果精确到1m). 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com