练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，为了测量某建筑物CE的高度，先在地面上用测角仪自A处测得建筑物顶部的仰角是45°，然后在水平地面上向建筑物前进了20m，此时自B处测得建筑物顶部的仰角是60°，已知测角仪的高度是1m，请你计算出该建筑物的高度（取 ≈1.732，结果精确到1m）．

    【答案】解：设CD为xm，
    在Rt△ADC中，∠CAD=45°，
    ∴AD=CD=xm，
    在Rt△BDC中，∠CBD=60°，
    ∴BD= = x，
    由题意得，x﹣ x=20，
    解得，x=10 +30，
    则该建筑物的高度为：10 +30+1≈48m．
    答：该建筑物的高度约为53m
    【解析】设CD为xm，根据正切的概念用x表示出AD、BD，根据题意列出方程，解方程即可求出CD，结合图形计算即可．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

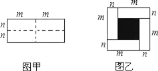
    【题目】已知图甲是一个长为2m，宽为2n的长方形，沿图甲中虚线用剪刀均匀分成四小块长方形，然后按图乙的形状拼成一个正方形．

    （1）图乙中阴影部分正方形的边长为　 　（用含字母m，n的整式表示）．

    （2）请用两种不同的方法求图乙中阴影部分的面积．

    方法一：　 　；

    方法二：　 　．

    （3）观察图乙，并结合（2）中的结论，你能写出下列三个整式：（m+n）2，（m﹣n）2，mn之间的等量关系吗？

    （4）根据（3）题中的等量关系，解决如下问题：若a+b=9，ab=5，求（a﹣b）2的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，在ABCD中，点E，F在对角线BD上，且BE=DF，

    求证：（1）AE=CF；（2）四边形AECF是平行四边形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在一个不透明的盒子中，共有“一红二白”三个球，它们除颜色外其余都相同．
    （1）从盒子中摸出1个球，是白球的概率是多少？
    （2）从盒子中摸出1个球，不放回再摸出1个球，请用画树状图或列表的方式表示出所有可能的结果，并求出摸出的恰好是“一红一白”的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了了解某市九年级学生学业考试体育成绩,现从中随机抽取部分学生的体育成绩进行分段(A:50分; B:49-45分;C:44-40分;D:39-30分;E:29-0分).每段包含最高分,不包含最低分,统计表如下,统计图如图所示.

    分数段

    频数(人)

    百分比

    根据上面提供的信息,回答下列问题:

    （1）在统计表中,的值为___, 的值为__,并将统计图补充完整.

    （2）成绩在40分以上定为优秀,那么该市今年10440名九年级学生中体育成绩为优秀的学生约有多少名?

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某人共收集邮票若干张，其中是2000年以前的国内外发行的邮票，是2001年国内发行的，是2002年国内发行的，此外尚有不足100张的国外邮票．求该人共有多少张邮票．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系，A（a，0），B（b，0），C（﹣1，2），且|2a+b+1|+（a+2b﹣4）2=0．

    （1）求a，b的值；

    （2）①在x轴的正半轴上存在一点M，使S△COM=△ABC的面积，求出点M的坐标；

    ②在坐标轴的其他位置是否存在点M，使△COM的面积=△ABC的面积仍然成立？若存在，请直接写出符合条件的点M的坐标为　 　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知AB∥CD.

    如图1,你能得出∠A＋∠E＋∠C=360°吗？

    如图2,猜想出∠A．∠C、∠E的关系式并说明理由.

    如图3,∠A．∠C、∠E的关系式又是什么?

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】“校园手机”现象越来越受到社会的关注．“寒假”期间，某校小记者随机调查了某地区若干名学生和家长对中学生带手机现象的看法，统计整理并制作了如下的统计图：

    （1）求这次调查的家长人数，并补全图1；

    （2）求图2中表示家长“赞成”的圆心角的度数；

    （3）已知某地区共6500名家长，估计其中反对中学生带手机的大约有多少名家长？

    查看答案和解析>>

    同步练习册答案