
【题目】先化简,再求值:3(2m+1)+2(m﹣1)2,其中m是方程x2+x﹣4=0的根.
科目:初中数学 来源: 题型:
【题目】某校规定:学生的数学学期综合成绩是由平时、期中和期末三项成绩按3:3:4的比例计算所得.若某同学本学期数学的平时、期中和期末成绩分别是90分,90分和85分,则他本学期数学学期综合成绩是分.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【探索新知】
如图1,射线OC在∠AOB的内部,图中共有3个角:∠AOB、∠AOC和∠BOC,若其中有一个角的度数是另一个角度数的两倍,则称射线OC是∠AOB的“妙分线”.
【解决问题】
(1)如图2,若∠MPN= ![]() ,且射线PQ是∠MPN的“妙分线”,则∠NPQ= ____ .(用含
,且射线PQ是∠MPN的“妙分线”,则∠NPQ= ____ .(用含![]() 的代数式表示出所有可能的结果)
的代数式表示出所有可能的结果)
【深入研究】
如图2,若∠MPN=54°,且射线PQ绕点P从PN位置开始,以每秒8°的速度顺时针旋转,当PQ与PN成![]() 时停止旋转,旋转的时间为t秒.
时停止旋转,旋转的时间为t秒.
(2)当t为何值时,射线PM是∠QPN的“妙分线”.
(3)若射线PM同时绕点P以每秒6°的速度顺时针旋转,并与PQ同时停止.请求出当射线PQ 是∠MPN的“妙分线”时t的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为推进“传统文化进校园”活动,某校准备成立“经典诵读”、“传统礼仪”、“民族器乐”和“地方戏曲”等四个课外活动小组.学生报名情况如图(每人只能选择一个小组):

(1)报名参加课外活动小组的学生共有 人,将条形图补充完整;
(2)扇形图中m= ,n= ;
(3)根据报名情况,学校决定从报名“经典诵读”小组的甲、乙、丙、丁四人中随机安排两人到“地方戏曲”小组,甲、乙恰好都被安排到“地方戏曲”小组的概率是多少?请用列表或画树状图的方法说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A样本的数据如下:72,73,76,76,77,78,78,78,B样本的数据恰好是A样本数据每个都加2,则A,B两个样本的下列统计量对应相同的是( )
A.平均数
B.标准差
C.中位数
D.众数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知线段AB=20cm,CD=2cm,线段CD在线段AB上运动,E、F分别是AC、BD的中点.
(1)若AC=4cm,则EF=_________cm.
(2)当线段CD在线段AB上运动时,试判断EF的长度是否发生变化?如果不变请求出EF的长度,如果变化,请说明理由.
(3)我们发现角的很多规律和线段一样,如图②已知![]() 在
在![]() 内部转动,OE、OF分别平分
内部转动,OE、OF分别平分![]() 在
在![]() ,则
,则![]() 、
、![]() 和
和![]() 有何关系,请直接写出_______________________.
有何关系,请直接写出_______________________.
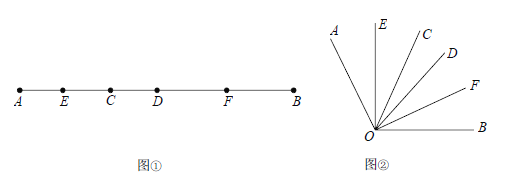
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,面积为28的平行四边形纸片ABCD中,AB=7,∠BAD=45°,按下列步骤进行裁剪和拼图.
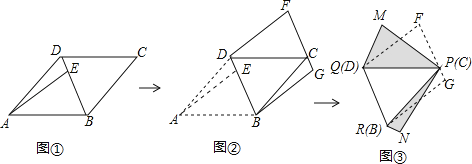
第一步:如图①,将平行四边形纸片沿对角线BD剪开,得到△ABD和△BCD纸片,再将△ABD纸片沿AE剪开(E为BD上任意一点),得到△ABE和△ADE纸片;
第二步:如图②,将△ABE纸片平移至△DCF处,将△ADE纸片平移至△BCG处;
第三步:如图③,将△DCF纸片翻转过来使其背面朝上置于△PQM处(边PQ与DC重合,△PQM和△DCF在DC同侧),将△BCG纸片翻转过来使其背面朝上置于△PRN处,(边PR与BC重合,△PRN和△BCG在BC同侧).
则由纸片拼成的五边形PMQRN中,对角线MN长度的最小值为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com