
【题目】如图①,已知线段AB=20cm,CD=2cm,线段CD在线段AB上运动,E、F分别是AC、BD的中点.
(1)若AC=4cm,则EF=_________cm.
(2)当线段CD在线段AB上运动时,试判断EF的长度是否发生变化?如果不变请求出EF的长度,如果变化,请说明理由.
(3)我们发现角的很多规律和线段一样,如图②已知![]() 在
在![]() 内部转动,OE、OF分别平分
内部转动,OE、OF分别平分![]() 在
在![]() ,则
,则![]() 、
、![]() 和
和![]() 有何关系,请直接写出_______________________.
有何关系,请直接写出_______________________.
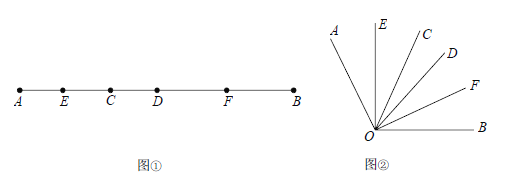
【答案】(1)11(2)11cm(3)![]()
【解析】试题分析:(1)由已知线段长度可以算出BD=14cm,由E、F分别是AC、BD的中点,可以得出EC=2cm,DF=7cm,从而计算出EF=11cm;(2)EF的长度不发生变化,由E、F分别是AC、BD的中点可得EC=![]() AC,DF=
AC,DF=![]() DB,所以EF=EC+CD+DF=
DB,所以EF=EC+CD+DF=![]() AC+CD+
AC+CD+![]() DB=
DB=![]() (AC+BD)+CD=
(AC+BD)+CD=![]() (AB-CD)+CD=
(AB-CD)+CD=![]() (AB+CD),计算出AB+CD的值即可;(3)∠EOF=
(AB+CD),计算出AB+CD的值即可;(3)∠EOF=![]() (∠AOC+∠DOB)+∠DOC=
(∠AOC+∠DOB)+∠DOC=![]() (∠AOB-∠DOC)+∠DOC=
(∠AOB-∠DOC)+∠DOC=![]() (∠AOB+∠DOC).
(∠AOB+∠DOC).
试题解析:
(1)∵AB=20cm,CD=2cm,AC=4cm,
∴ BD=AB-AC-CD= 20-2-4=14cm,
∵E、F分别是AC、BD的中点,
∴EC=2cm,DF=7cm,
∴EF=2+2+7=11cm;
(2)EF的长度不发生变化,
∵E、F分别是AC、BD的中点,
∴EC=![]() AC,DF=
AC,DF=![]() DB,
DB,
∴EF=EC+CD+DF
=![]() AC+CD+
AC+CD+![]() DB
DB
=![]() (AC+BD)+CD
(AC+BD)+CD
=(AB-CD)+CD
=![]() (AB+CD),
(AB+CD),
∵AB = 20cm, CD = 2cm,
∴EF =![]() (20+2)=11cm;
(20+2)=11cm;
(3)∠EOF=![]() (∠AOB+∠COD).
(∠AOB+∠COD).


 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:初中数学 来源: 题型:
【题目】如图,已知顶点为(﹣3,﹣6)的抛物线y=ax2+bx+c经过点(﹣1,﹣4),则下列结论中错误的是( )

A. b2>4ac
B. ax2+bx+c≥﹣6
C. 若点(﹣2,m),(﹣5,n)在抛物线上,则m>n
D. 关于x的一元二次方程ax2+bx+c=﹣4的两根为﹣5和﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为增强学生的身体素质,教育行政部门规定每位学生每天参加户外活动的平均时间不少于1小时. 为了解学生参加户外活动的情况,对部分学生参加户外活动的时间进行抽样调查,并将调查结果绘制作成如下两幅不完整的统计图,

请你根据图中提供的信息解答下列问题:
(1)在这次调查中共调查了多少名学生?
(2)求户外活动时间为1.5小时的人数,并补充频数分布直方图;
(3)户外活动时间的众数和中位数分别是多少?
(4)若该市共有20000名学生,大约有多少学生户外活动的平均时间符合要求?
查看答案和解析>>
科目:初中数学 来源: 题型:
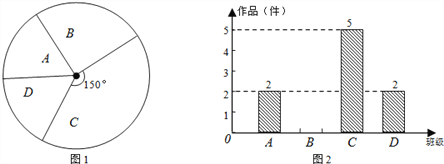
【题目】我市某中学艺术节期间,向学校学生征集书画作品.九年级美术李老师从全年级14个班中随机抽取了A、B、C、D 4个班,对征集到的作品的数量进行了分析统计,制作了如下两幅不完整的统计图.
(1)李老师采取的调查方式是 (填“普查”或“抽样调查”),李老师所调查的4个班征集到作品共 件,其中B班征集到作品为 件,请把图2补充完整.
(2)如果全年级参展作品中有4件获得一等奖,其中有2名作者是男生,2名作者是女生.现在要在抽两人去参加学校总结表彰座谈会,求恰好抽中一男一女的概率.(要求用树状图或列表法写出分析过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=24cm,BC=26cm,点P从点A出发,以1cm/s的速度向点D运动;点Q从点C同时出发,以3cm/s的速度向点B运动.规定其中一个动点到达端点时,另一个动点也随之停止运动,设运动时间为t(s). 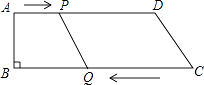
(1)当t为何值时,PQ∥CD?
(2)当t为何值时,PQ=CD?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上点B表示的为-5,点A是数轴上一点,且AB=12,动点P从点A出发,以每秒1个单位长度的速度沿数轴向右匀速运动,动点H从点B出发,以每秒2个单位长度的速度沿数轴向右匀速运动,设运动时间为![]() (
(![]() )秒.
)秒.
(1)写出数轴上点A表示的数 ;
(2)当动点P,H同时从点A和点B出发,运动![]() 秒时,点P表示的数 ;点H表示的数 ;(用含
秒时,点P表示的数 ;点H表示的数 ;(用含![]() 的代数式表示)
的代数式表示)
(3)动点P、H同时出发,问点H运动多少秒时追上点P?
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com