
����Ŀ����ͼ����֪�����ϵ�B��ʾ��Ϊ-5����A��������һ�㣬��AB=12������P�ӵ�A��������ÿ��1����λ���ȵ��ٶ����������������˶�������H�ӵ�B��������ÿ��2����λ���ȵ��ٶ����������������˶������˶�ʱ��Ϊ![]() ��
��![]() ���룮
���룮
��1��д�������ϵ�A��ʾ������������������
��2��������P��Hͬʱ�ӵ�A�͵�B�������˶�![]() ��ʱ����P��ʾ���� ����H��ʾ���� �����ú�
��ʱ����P��ʾ���� ����H��ʾ���� �����ú�![]() �Ĵ���ʽ��ʾ��
�Ĵ���ʽ��ʾ��
��3������P��Hͬʱ�������ʵ�H�˶�������ʱ�ϵ�P��
![]()
���𰸡���1��7����2��7+t,2t-5;(3)12��.
�������������������1�������������빫ʽ����������ϵ�A��ʾ������
��2����������֮��ľ��빫ʽ�����P��ʾ�������H��ʾ������
��3�����������г�����2t-5=7+ ![]() �� ��⼴��.
�� ��⼴��.
�����������1���������ϵ�B��ʾ����Ϊ-5��A��������һ�㣬��AB=12��
��AO=7��
�������ϵ�A��ʾ����Ϊ��7;
��2����P��ʾ����7+ ![]() ,��H��ʾ����2
,��H��ʾ����2![]() -5.
-5.
��3����������ã�
2t-5=7+ ![]() ��
��
���![]() =12��
=12��
�𣺵�H�˶�12��ʱ�ϵ�P��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�٣���֪�߶�AB=20cm��CD=2cm���߶�CD���߶�AB���˶���E��F�ֱ���AC��BD���е�.
��1����AC=4cm����EF=_________cm.
��2�����߶�CD���߶�AB���˶�ʱ�����ж�EF�ij����Ƿ����仯��������������EF�ij��ȣ�����仯����˵������.
��3�����Ƿ��ֽǵĺܶ���ɺ��߶�һ������ͼ����֪![]() ��
��![]() �ڲ�ת����OE��OF�ֱ�ƽ��
�ڲ�ת����OE��OF�ֱ�ƽ��![]() ��
��![]() ����
����![]() ��
��![]() ��
��![]() �кι�ϵ����ֱ��д��_______________________.
�кι�ϵ����ֱ��д��_______________________.
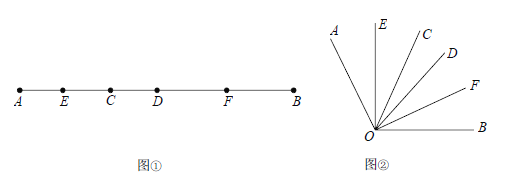
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����Ϊ28��ƽ���ı���ֽƬABCD�У�AB=7����BAD=45�㣬�����в�����вü���ƴͼ��
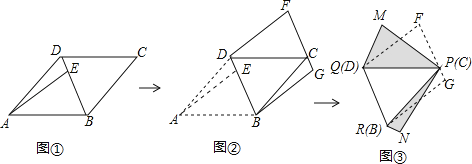
��һ������ͼ�٣���ƽ���ı���ֽƬ�ضԽ���BD�������õ���ABD�͡�BCDֽƬ���ٽ���ABDֽƬ��AE������EΪBD������һ�㣩���õ���ABE�͡�ADEֽƬ��
�ڶ�������ͼ�ڣ�����ABEֽƬƽ������DCF��������ADEֽƬƽ������BCG����
����������ͼ�ۣ�����DCFֽƬ��ת����ʹ�䱳�泯�����ڡ�PQM������PQ��DC�غϣ���PQM�͡�DCF��DCͬ�ࣩ������BCGֽƬ��ת����ʹ�䱳�泯�����ڡ�PRN��������PR��BC�غϣ���PRN�͡�BCG��BCͬ�ࣩ��
����ֽƬƴ�ɵ������PMQRN�У��Խ���MN���ȵ���СֵΪ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ж�����˵������
��1������һ�����ݣ���ô�������ݵ������п��ܲ�Ψһ������
��2������һ�����ݣ���ô�������ݵ�ƽ����һ�������������е�һ������
����
��3��n��������λ��һ������n�����е�ijһ��������
��4����9�����ݣ�x1��x2��������x9 �� ��ƽ����Ϊm���ı���S�� ���㹫ʽΪ�� ![]() ������
������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ŀǰ���ܵ��ڸ����������ռ�ʹ�ã�ij��һ�̳�Ϊ��Ӧ���٣��ƹ����ۣ����̳��ƻ���3800Ԫ�������ֽ��ܵƹ�120ֻ�������ֽ��ܵƵĽ��ۡ��ۼ����±���

��1����ס��������ͺŽ��ܵƸ�������ֻ��
��2��ȫ������120ֻ���ܵƺ��̳���������Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�ı���ABCD�������Σ���E��F�ֱ�������AB������BC�ϣ�AE=BF��DE��AF���ڵ�O.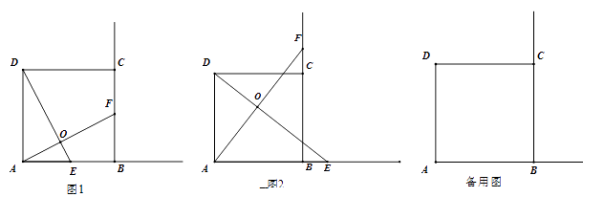
��1����ͼ1������E��F�ֱ����߶�AB��BC��ʱ�����߶�DE���߶�AF��������ϵ�� �� λ�ù�ϵ��.
��2�����߶�AE��AF����ƽ����FG������DG.
����ͼ2������E��AB�ӳ�����ʱ����ȫͼ�Σ�д��AD��AE��DG֮���������ϵ.
����DG= ![]() ��
�� ![]() ��ֱ��д��AD����
��ֱ��д��AD����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����з����У��ԩ�2Ϊ��ķ�����( )
A. 3x+1��2x��1B. 3x��2��2x
C. 5x��3��6x��2D. 4x��1��2x+3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
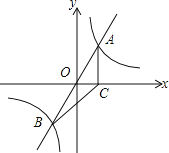
����Ŀ����ͼ��ֱ��y=mx��˫����y=![]() �ཻ��A��B���㣬A�������Ϊ��1��2����AC��x����C������BC��
�ཻ��A��B���㣬A�������Ϊ��1��2����AC��x����C������BC��
��1�����������ı���ʽ��
��2������ͼ��ֱ��д����mx��![]() ʱ��x��ȡֵ��Χ��
ʱ��x��ȡֵ��Χ��
��3����ƽ�����Ƿ����һ��D��ʹ�ı���ABDCΪƽ���ı��Σ������ڣ��������D���ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com