
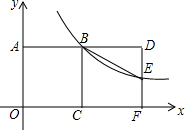
 如图,边长为2的正方形ABCO的顶点C、A分别在x轴、y轴上,函数y=$\frac{k}{x}$(x>0)的图象经过点B,把正方形ABCO沿BC翻折得到正方形BCFD,DF交这个函数的图象于点E,连结BE.
如图,边长为2的正方形ABCO的顶点C、A分别在x轴、y轴上,函数y=$\frac{k}{x}$(x>0)的图象经过点B,把正方形ABCO沿BC翻折得到正方形BCFD,DF交这个函数的图象于点E,连结BE.分析 (1)根据正方形的面积公式可求得点B的坐标,代入函数y=$\frac{k}{x}$中从而求得k值;
(2)先根据正方形的性质求得点E的横坐标,代入反比例函数解析式求得其坐标,利用梯形的面积公式即可得到结果.
解答 解:(1)由题意,知B(2,2),
∵函数$y=\frac{k}{x}$(x>0)的图象经过点B,
∴2=$\frac{k}{2}$,
∴k=4;
(2)由题意,知CF=2,OF=4,
当x=4时,y=$\frac{4}{4}$=1,
∴E(4,1).∴EF=1,
∴四边形BCFE的面积为$\frac{(1+2)×2}{2}=3$.
点评 此题考查了反比例函数与一次函数的性质,综合性比较强,注意反比例函数上的点向x轴y轴引垂线形成的矩形面积等于反比例函数的k值.要会熟练地运用待定系数法求函数解析式,这是基本的计算能力.


科目:初中数学 来源: 题型:选择题
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 没有实数根 | D. | 以上三种情况都有可能 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
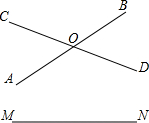 如图,已知相交直线AB和CD及另一直线MN,如果要在MN上找出与AB,CD距离相等的点,方法是分别作∠AOD及∠AOC的平分线OE与OF,这样的点至少有1个,最多有2个.
如图,已知相交直线AB和CD及另一直线MN,如果要在MN上找出与AB,CD距离相等的点,方法是分别作∠AOD及∠AOC的平分线OE与OF,这样的点至少有1个,最多有2个.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
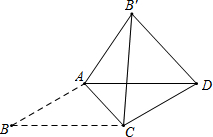 如图,平行四边形ABCD中,∠B=30°,AB≠BC,将△ABC沿AC翻折至△AB′C,连接B′D,若AB=2$\sqrt{3}$,∠AB′D=75°,则:①∠CB′D=45°;②BC=3$+\sqrt{3}$.
如图,平行四边形ABCD中,∠B=30°,AB≠BC,将△ABC沿AC翻折至△AB′C,连接B′D,若AB=2$\sqrt{3}$,∠AB′D=75°,则:①∠CB′D=45°;②BC=3$+\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
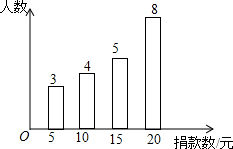 某校学生会干部对校学生会倡导的“助残”自愿捐款活动进行抽样调查,得到一组学生捐款情况的数据,根据这组数据绘制成如图所示的统计图.
某校学生会干部对校学生会倡导的“助残”自愿捐款活动进行抽样调查,得到一组学生捐款情况的数据,根据这组数据绘制成如图所示的统计图.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{16}$=±4 | B. | $\sqrt{(-\frac{1}{3})^{2}}$=$\frac{1}{3}$ | C. | $\sqrt{-1\frac{7}{9}}$=-1$\frac{1}{3}$ | D. | $\root{3}{-9}$=-3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com