
【题目】如图,等腰![]() ,点
,点![]() 为斜边
为斜边![]() 上,作
上,作![]() 与
与![]() 相切于点
相切于点![]() ,交
,交![]() 于点
于点![]() 、点
、点![]() .已知
.已知![]() ,
,![]() ,则
,则![]() 的长度为( )
的长度为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
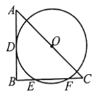
连接OD,OF,过O作OG⊥EF于G,根据切线的性质得到∠ODB=90°,推出四边形BGOD是矩形,△ADO与△CGO是等腰直角三角形,设OD=BG=OF=x,则BD=OG=CG=9![]() x,则EG=FG=CG
x,则EG=FG=CG![]() CF=8
CF=8![]() x,根据勾股定理OF2=OG2+FG2,即可求出半径,然后得到BE的长度.
x,根据勾股定理OF2=OG2+FG2,即可求出半径,然后得到BE的长度.
解:如图,连接OD,OF,过O作OG⊥EF于G,
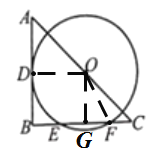
∵AB是切线,
∴OD⊥AB,
∵OG⊥BC,△ABC是等腰直角三角形,
∴四边形BGOD是矩形,△AOD、△OCG是等腰直角三角形.
∴OD=BG=OF,BD=OG=CG,EG=FG,
∵AB=BC=9,则设OD=BG=OF=x,
∴OG=CG=9![]() x,FG=CG
x,FG=CG![]() ,
,
在Rt△OGF中,OF2=OG2+FG2,
∴![]() ,
,
解得:![]() 或
或![]() (舍去);
(舍去);
∴BG=5,EG=FG=3,
∴BE=BG![]() EG=5
EG=5![]() 3=2;
3=2;
故选择:B.


 寒假学与练系列答案
寒假学与练系列答案科目:初中数学 来源: 题型:
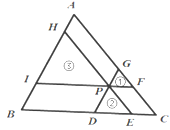
【题目】如图,过![]() 内一点分别作三边的平行线,形成三个小三角形①、②、③,如果这三个小三角形面积分别为1、4、9,则
内一点分别作三边的平行线,形成三个小三角形①、②、③,如果这三个小三角形面积分别为1、4、9,则![]() 的面积为____________
的面积为____________
 .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市举行知识大赛,A校、B校各派出5名选手组成代表队参加决赛,两校派出选手的决赛成绩如图所示.
![]() 根据图示填写下表:
根据图示填写下表:
平均数 | 中位数 | 众数 | |
A校 | ______ | 85 | ______ |
B校 | 85 | ______ | 100 |
![]() 结合两校成绩的平均数和中位数,分析哪个学校的决赛成绩较好;
结合两校成绩的平均数和中位数,分析哪个学校的决赛成绩较好;
![]() 计算两校决赛成绩的方差,并判断哪个学校代表队选手成绩较为稳定.
计算两校决赛成绩的方差,并判断哪个学校代表队选手成绩较为稳定.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在斜坡顶部有一铁塔AB,B是CD的中点,CD是水平的.在阳光的照射下,塔影DE留在斜坡面上.在同一时刻,小明站在点E处,其影子EF在直线DE上,小华站在点G处,影子GH在直线CD上,他们的影子长分别为2 m和1 m.已知CD=12 m,DE=18 m,小明和小华身高均为1.6 m,那么塔高AB为多少?
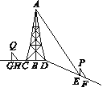
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,梯形ABCD中,AB//CD,且AB=2CD,E,F分别是AB,BC的中点.
EF与BD相交于点M.

(1)求证:△EDM∽△FBM;
(2)若DB=9,求BM.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售的某种商品每件的标价是![]() 元,若按标价的八折销售,仍可盈利
元,若按标价的八折销售,仍可盈利![]() ,此时该种商品每星期可卖出
,此时该种商品每星期可卖出![]() 件,市场调查发现:在八折销售的基础上,该种商品每降价
件,市场调查发现:在八折销售的基础上,该种商品每降价![]() 元,每星期可多卖
元,每星期可多卖![]() 件.设每件商品降价
件.设每件商品降价![]() 元(
元(![]() 为整数),每星期的利润为
为整数),每星期的利润为![]() 元
元
(1)求该种商品每件的进价为多少元?
(2)当售价为多少时,每星期的利润最大?最大利润是多少?
(3)2019年2月该种商品每星期的售价均为每件![]() 元,若2019年2月的利润不低于
元,若2019年2月的利润不低于![]() 元,请求出
元,请求出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数![]() 的图象交x轴于点A,B(点A在点B的左侧).
的图象交x轴于点A,B(点A在点B的左侧).
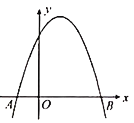
(1)求点A,B的坐标,并根据该函数图象写出y≥0时x的取值范围;
(2)把点B向上平移m个单位得点B1.若点B1向左平移n个单位,将与该二次函数图象上的点B2重合;若点B1向左平移(n+6)个单位,将与该二次函数图象上的点B3重合.已知m>0,n>0,求m,n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
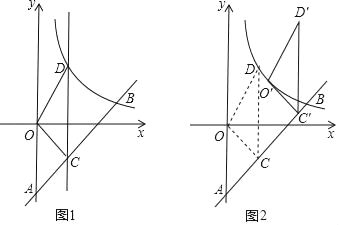
【题目】如图1,一次函数y=kx﹣6(k≠0)的图象与y轴交于点A,与反比例函数y=![]() (x>0)的图象交于点B(4,b).
(x>0)的图象交于点B(4,b).
(1)b= ;k= ;
(2)点C是线段AB上一点,过点C且平行于y轴的直线l交该反比例函数的图象于点D,连接OC,OD,BD,若四边形OCBD的面积S四边形OCBD=![]() ,求点C的坐标;
,求点C的坐标;
(3)将第(2)小题中的△OCD沿射线AB方向平移一定的距离后,得到△O'C'D',若点O的对应点O'恰好落在该反比例函数图象上(如图2),求此时点D的对应点D'的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com