
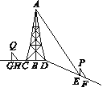
【题目】如图,在斜坡顶部有一铁塔AB,B是CD的中点,CD是水平的.在阳光的照射下,塔影DE留在斜坡面上.在同一时刻,小明站在点E处,其影子EF在直线DE上,小华站在点G处,影子GH在直线CD上,他们的影子长分别为2 m和1 m.已知CD=12 m,DE=18 m,小明和小华身高均为1.6 m,那么塔高AB为多少?
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
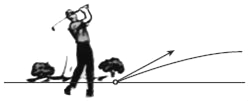
【题目】如图,以40m/s的速度将小球沿与地面成30°角的方向击出时,小球的飞行路线是一条抛物线.如果不考虑空气阻力,小球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有函数关系h=20t﹣5t2.
(1)小球飞行时间是多少时,小球最高?最大高度是多少?
(2)小球飞行时间t在什么范围时,飞行高度不低于15m?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,半径为1的⊙P的圆心在(﹣4,0)处.若⊙P以每秒1个单位长度,沿x轴向右匀速运动.设运动时间为t秒,当⊙P上有且只有2个点到y轴的距离为2,则t的取值范围是_____.
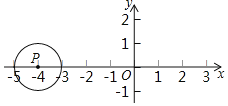
查看答案和解析>>
科目:初中数学 来源: 题型:
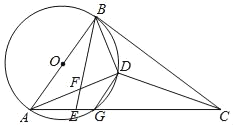
【题目】如图:AB是⊙O的直径,AC交⊙O于G,E是AG上一点,D为△BCE内心,BE交AD于F,且∠DBE=∠BAD.
(1)求证:BC是⊙O的切线;
(2)求证:DF=DG.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,点P是边长为2的正方形ABCD的对角线BD上的动点,过点P分别作PE⊥BC于点E,PF⊥DC于点F,连接AP并延长,交射线BC于点H,交射线DC于点M,连接EF交AH于点G,当点P在BD上运动时(不包括B、D两点),以下结论中:①MF=MC;②AP=EF;③AH⊥EF;④AP2=PMPH;⑤EF的最小值是![]() .其中正确结论有( )
.其中正确结论有( )
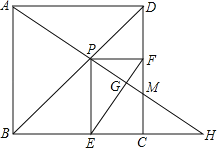
A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一张长方形纸板的四个角上分别剪掉2个小正方形和2个小长方形(阴影部分即剪掉的部分),剩余的部分可以折成一个有盖的长方体盒子(纸板的厚度忽略不计).若长方形纸板边长分别为40cm和30cm,且折成的长方体盒子表面积是950cm2,此时长方体盒子的体积为_____cm3.
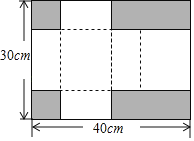
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于点C,且OC=2OB则下列结论:①abc<0;②a+b+c>0;③ac﹣2b+4=0;④OAOB=![]() ,其中正确的结论有( )
,其中正确的结论有( )
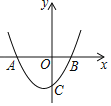
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】宝鸡市某学校在“行读石鼓阁”研学活动中,参观了我市中华石鼓园,石鼓阁是宝鸡城市新地标.建筑面积7200平方米,为我国西北第一高阁.小亮想知道石鼓阁的高是多少,他和同学小明对石鼓阁进行测量.测量方案如下:如图,小明在小亮和“石鼓阁”之间的直线BM上平放一平面镜,在镜面上做了一个标记,这个标记在直线BM上的对应位置为点C,镜子不动,小明看着镜面上的标记,他来回走动,走到点D时,看到“石鼓阁”顶端点A在镜面中的像与镜面上的标记重合,这时,测得小明眼睛与地面的高度ED=1.6米,CD=2.2米,然后,在阳光下,小亮从D点沿DM方向走了29.6米,此时“石鼓阁”影子与小亮的影子顶端恰好重合,测得小亮身高1.6米,影长FH=3.2米.已知AB⊥BM,ED⊥BM,GF⊥BM,其中,测量时所使用的平面镜的厚度忽略不计,请你根据题中提供的相关信息,求出“石鼓阁”的高AB的长度.
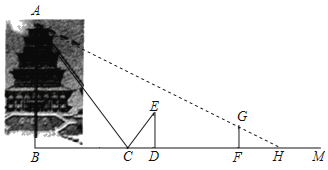
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com