
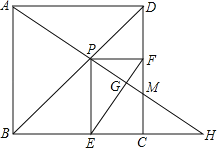
【题目】如图所示,点P是边长为2的正方形ABCD的对角线BD上的动点,过点P分别作PE⊥BC于点E,PF⊥DC于点F,连接AP并延长,交射线BC于点H,交射线DC于点M,连接EF交AH于点G,当点P在BD上运动时(不包括B、D两点),以下结论中:①MF=MC;②AP=EF;③AH⊥EF;④AP2=PMPH;⑤EF的最小值是![]() .其中正确结论有( )
.其中正确结论有( )
A.2个B.3个C.4个D.5个
【答案】C
【解析】
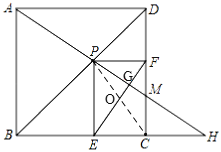
由点P为BD中点时,MC=0≠MF,可得①错误;连接PC,交EF于O,由点P在BD上,可得AP=PC,根据PF⊥CD,PE⊥BC,∠BCF=90°可得四边形PECF是矩形,可得EF=PC,即判断②正确;利用SSS可证明△APD≌△CPD,可得∠DAP=∠DCP,由矩形的性质可得∠OCF=∠OFC,即可证明∠DAP=∠OFC,可得∠DAP+∠AMD=∠OFC+∠AMD=90°,即可判断③正确;根据平行线的性质可得∠DAP=∠H,可得∠DCP=∠H,由∠HPC是公共角可证明△CPM∽△HPC,根据相似三角形的性质可得![]() ,根据PC=AP即可判断④正确,当PC⊥BD时PC的值最小,根据等腰直角三角形的性质可求出PC的最小值为
,根据PC=AP即可判断④正确,当PC⊥BD时PC的值最小,根据等腰直角三角形的性质可求出PC的最小值为![]() ,根据EF=PC即可判断⑤正确;综上即可得答案.
,根据EF=PC即可判断⑤正确;综上即可得答案.
当点P为BD中点时,点M与点C重合,MC=0≠MF,故①错误,
连接PC,交EF于O,
∵点P在BD上,BD为正方形ABCD的对角线,
∴AP=PC,
∵PF⊥CD,PE⊥BC,∠BCF=90°,
∴四边形PECF是矩形,
∴EF=PC,
∴AP=EF,故②正确,
∵AD=CD,AP=PC,PD=PD,
∴△APD≌△CPD,
∴∠DAP=∠DCP,
∵四边形PECF是矩形,
∴∠OCF=∠OFC,
∴∠DAP=∠OFC,
∴∠DAP+∠AMD=∠OFC+∠AMD=90°,
∴∠FGM=90°,即AH⊥EF,故③正确,
∵AD//BH,
∴∠DAP=∠H,
∵∠DAP=∠DCP,
∴∠MCP=∠H,
∵∠CPH为公共角,
∴△CPM∽△HPC,
∴![]() ,
,
∵AP=PC,
∴AP2= PMPH,故④正确,
当PC⊥BD时,PC有最小值,PC=![]() BD=
BD=![]() ,
,
∵PC=EF
∴EF的最小值为![]() ,故⑤正确,
,故⑤正确,
综上所述:正确的结论有②③④⑤,共4个,
故选C.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,P是正三角形ABC内的一点,且PA=6,PB=8,PC=10.若将△PAC绕点A逆时针旋转后,得到△P′AB.
(1)求点P与点P′之间的距离;
(2)求∠APB的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
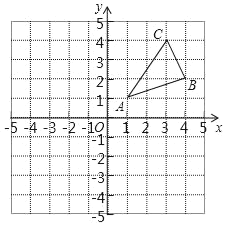
【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
(1)请画出△ABC向左平移5个单位长度后得到的△A1B1C1;
(2)请画出△ABC关于原点对称的△A2B2C2;并写出点A2、B2、C2坐标;
(3)请画出△ABC绕O逆时针旋转90°后的△A3B3C3;并写出点A3、B3、C3坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市举行知识大赛,A校、B校各派出5名选手组成代表队参加决赛,两校派出选手的决赛成绩如图所示.
![]() 根据图示填写下表:
根据图示填写下表:
平均数 | 中位数 | 众数 | |
A校 | ______ | 85 | ______ |
B校 | 85 | ______ | 100 |
![]() 结合两校成绩的平均数和中位数,分析哪个学校的决赛成绩较好;
结合两校成绩的平均数和中位数,分析哪个学校的决赛成绩较好;
![]() 计算两校决赛成绩的方差,并判断哪个学校代表队选手成绩较为稳定.
计算两校决赛成绩的方差,并判断哪个学校代表队选手成绩较为稳定.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线经过点A(﹣1,0),B(4,0),C(0,2)三点,点D与点C关于x轴对称,点P是线段AB上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线l交抛物线于点Q,交直线BD于点M.
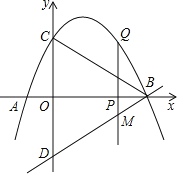
(1)求该抛物线所表示的二次函数的表达式;
(2)求证:∠ACB=90°;
(3)在点P运动过程中,是否存在点Q,使得△BQM是直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由;
(4)连接AC,将△AOC绕平面内某点H顺时针旋转90°,得到△A1O1C1,点A、O、C的对应点分别是点A1、O1、C1、若△A1O1C1的两个顶点恰好落在抛物线上,那么我们就称这样的点为“和谐点”,请直接写出“和谐点”的个数和点A1的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
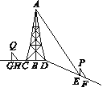
【题目】如图,在斜坡顶部有一铁塔AB,B是CD的中点,CD是水平的.在阳光的照射下,塔影DE留在斜坡面上.在同一时刻,小明站在点E处,其影子EF在直线DE上,小华站在点G处,影子GH在直线CD上,他们的影子长分别为2 m和1 m.已知CD=12 m,DE=18 m,小明和小华身高均为1.6 m,那么塔高AB为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,梯形ABCD中,AB//CD,且AB=2CD,E,F分别是AB,BC的中点.
EF与BD相交于点M.

(1)求证:△EDM∽△FBM;
(2)若DB=9,求BM.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数![]() 的图象交x轴于点A,B(点A在点B的左侧).
的图象交x轴于点A,B(点A在点B的左侧).
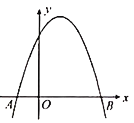
(1)求点A,B的坐标,并根据该函数图象写出y≥0时x的取值范围;
(2)把点B向上平移m个单位得点B1.若点B1向左平移n个单位,将与该二次函数图象上的点B2重合;若点B1向左平移(n+6)个单位,将与该二次函数图象上的点B3重合.已知m>0,n>0,求m,n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车租贸公司共有汽车50辆,市场调查表明,当租金为每辆每日200元时可全部租出,当租金每提高10元,租出去的车就减少2辆.
(1)当租金提高多少元时,公司的每日收益可达到10120元?
(2)公司领导希望日收益达到10160元,你认为能否实现?若能,求出此时的租金,若不能,请说明理由,
(3)汽车日常维护要定费用,已知外租车辆每日维护费为100元未租出的车辆维护费为50元,当租金为多少元时,公司的利润恰好为5500元?(利润=收益﹣维护费)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com