
ЁОЬтФПЁПШчЭМЃЌвбжЊХзЮяЯпОЙ§ЕуAЃЈЉ1ЃЌ0ЃЉЃЌBЃЈ4ЃЌ0ЃЉЃЌCЃЈ0ЃЌ2ЃЉШ§ЕуЃЌЕуDгыЕуCЙигкxжсЖдГЦЃЌЕуPЪЧЯпЖЮABЩЯЕФвЛИіЖЏЕуЃЌЩшЕуPЕФзјБъЮЊЃЈmЃЌ0ЃЉЃЌЙ§ЕуPзїxжсЕФДЙЯпlНЛХзЮяЯпгкЕуQЃЌНЛжБЯпBDгкЕуMЃЎ
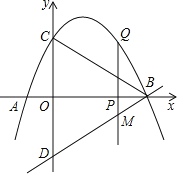
ЃЈ1ЃЉЧѓИУХзЮяЯпЫљБэЪОЕФЖўДЮКЏЪ§ЕФБэДяЪНЃЛ
ЃЈ2ЃЉЧѓжЄЃКЁЯACB=90ЁуЃЛ
ЃЈ3ЃЉдкЕуPдЫЖЏЙ§ГЬжаЃЌЪЧЗёДцдкЕуQЃЌЪЙЕУЁїBQMЪЧжБНЧШ§НЧаЮЃПШєДцдкЃЌЧѓГіЕуQЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ4ЃЉСЌНгACЃЌНЋЁїAOCШЦЦНУцФкФГЕуHЫГЪБеыа§зЊ90ЁуЃЌЕУЕНЁїA1O1C1ЃЌЕуAЁЂOЁЂCЕФЖдгІЕуЗжБ№ЪЧЕуA1ЁЂO1ЁЂC1ЁЂШєЁїA1O1C1ЕФСНИіЖЅЕуЧЁКУТфдкХзЮяЯпЩЯЃЌФЧУДЮвУЧОЭГЦетбљЕФЕуЮЊЁАКЭаГЕуЁБЃЌЧыжБНгаДГіЁАКЭаГЕуЁБЕФИіЪ§КЭЕуA1ЕФКсзјБъЃЎ
ЁОД№АИЁПЃЈ1ЃЉyЃНЉ![]() +x+2ЃЛЃЈ2ЃЉМћНтЮіЃЛЃЈ3ЃЉQЃЈ3ЃЌ2ЃЉЛђQЃЈЉ1ЃЌ0ЃЉЃЛЃЈ4ЃЉСНИіКЭаГЕуЃЛ A1ЕФКсзјБъЪЧ1ЃЛ
+x+2ЃЛЃЈ2ЃЉМћНтЮіЃЛЃЈ3ЃЉQЃЈ3ЃЌ2ЃЉЛђQЃЈЉ1ЃЌ0ЃЉЃЛЃЈ4ЃЉСНИіКЭаГЕуЃЛ A1ЕФКсзјБъЪЧ1ЃЛ![]() .
.
ЁОНтЮіЁП
ЃЈ1ЃЉАбЕуAЃЈ1ЃЌ0ЃЉЁЂBЃЈ4ЃЌ0ЃЉЁЂCЃЈ0ЃЌ3ЃЉШ§ЕуЕФзјБъДњШыКЏЪ§НтЮіЪНЃЌРћгУД§ЖЈЯЕЪ§ЗЈЧѓНтЃЛ
ЃЈ2ЃЉЯШЧѓГіABЁЂACЁЂBCЕФГЄЖШЃЌИљОнЙДЙЩЖЈРэМДПЩжЄУї;
ЃЈ3ЃЉЗжСНжжЧщПіЗжБ№ЬжТлЃЌЕБЁЯQBMЃН90ЁуЛђЁЯMQBЃН90ЁуЃЌМДПЩЧѓЕУQЕуЕФзјБъЃЎ
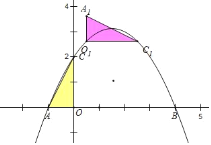
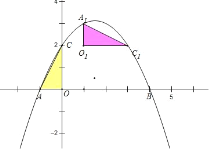
ЃЈ4ЃЉСНИіКЭаГЕуЃЛAOЃН1ЃЌOCЃН2ЃЌЩшA1ЃЈxЃЌyЃЉЃЌдђC1ЃЈx+2ЃЌyЉ1ЃЉЃЌO1ЃЈxЃЌyЉ1ЃЉЃЌЕБA1ЁЂC1дкХзЮяЯпЩЯЪБКЭO1ЁЂC1дкХзЮяЯпЩЯЪБЃЌЗжСНжжЧщПіСаЗНГЬзщПЩЕУA1ЕФКсзјБъ.
ЃЈ1ЃЉЩшХзЮяЯпНтЮіЪНЮЊyЃНax2+bx+cЃЌ
НЋЕуAЃЈЉ1ЃЌ0ЃЉЃЌBЃЈ4ЃЌ0ЃЉЃЌCЃЈ0ЃЌ2ЃЉДњШыНтЮіЪНЃЌ
Ёр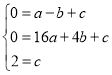 ЃЌЁр
ЃЌЁр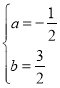 ЃЌ
ЃЌ
Ёр![]() ЃЛ
ЃЛ
ЃЈ2ЃЉжЄУїЃКЁп![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ Ёр
ЃЌ Ёр![]() ЃЌМДЁЯACB=90ЁуЃЛ
ЃЌМДЁЯACB=90ЁуЃЛ
ЃЈ3ЃЉЁпЕуCгыЕуDЙигкxжсЖдГЦЃЌЁрDЃЈ0ЃЌЉ2ЃЉЃЎ
ЩшжБЯпBDЕФНтЮіЪНЮЊyЃНkxЉ2ЃЎ
ЁпНЋЃЈ4ЃЌ0ЃЉДњШыЕУЃК4kЉ2ЃН0ЃЌ
ЁрkЃН![]() ЃЎЁржБЯпBDЕФНтЮіЪНЮЊyЃН
ЃЎЁржБЯпBDЕФНтЮіЪНЮЊyЃН![]() xЉ2ЃЎ
xЉ2ЃЎ
ЕБPЕугыAЕужиКЯЪБЃЌЁїBQMЪЧжБНЧШ§НЧаЮЃЌДЫЪБQЃЈЉ1ЃЌ0ЃЉЃЛ
ЕБBQЁЭBDЪБЃЌЁїBQMЪЧжБНЧШ§НЧаЮЃЌ
дђжБЯпBQЕФжБЯпНтЮіЪНЮЊyЃНЉ2x+8ЃЌ
Ёр![]() ЃЌПЩЧѓxЃН3ЛђxЃН4ЃЈЩсЃЉ
ЃЌПЩЧѓxЃН3ЛђxЃН4ЃЈЩсЃЉ
ЁрxЃН3ЃЛ
ЁрQЃЈ3ЃЌ2ЃЉЛђQЃЈЉ1ЃЌ0ЃЉЃЛ
ЃЈ4ЃЉСНИіКЭаГЕуЃЛ
AOЃН1ЃЌOCЃН2ЃЌ
ЩшA1ЃЈxЃЌyЃЉЃЌдђC1ЃЈx+2ЃЌyЉ1ЃЉЃЌO1ЃЈxЃЌyЉ1ЃЉЃЌ
ЂйЕБA1ЁЂC1дкХзЮяЯпЩЯЪБЃЌ
Ёр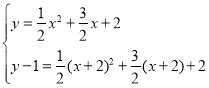 ЃЌЁр
ЃЌЁр![]() ЃЌ
ЃЌ
ЁрA1ЕФКсзјБъЪЧ1ЃЛ
ЕБO1ЁЂC1дкХзЮяЯпЩЯЪБЃЌ
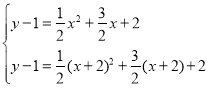 ЃЌЁр
ЃЌЁр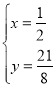 ЃЌ
ЃЌ
ЁрA1ЕФКсзјБъЪЧ![]() .
.



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊе§ЗНаЮABCDжаЃЌBEЦНЗжЁЯDBCЧвНЛCDБпгкЕуEЃЌНЋЁїBCEШЦЕуCЫГЪБеыа§зЊЕНЁїDCFЕФЮЛжУЃЌВЂбгГЄBEНЛDFгкЕуGЃЎ
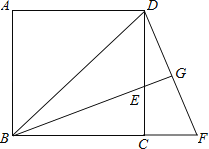
ЃЈ1ЃЉЧѓжЄЃКЁїBDGЁзЁїDEGЃЛ
ЃЈ2ЃЉШєEGBG=4ЃЌЧѓBEЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
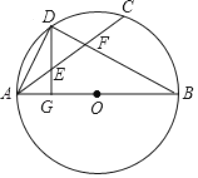
ЁОЬтФПЁПШчЭМЃЌABЮЊЁбOжБОЖЃЌDЮЊЛЁACЕФжаЕуЃЌDGЁЭABгкGЃЌНЛACгкEЃЌACЁЂBDЯрНЛгкFЃЎ
ЃЈ1ЃЉЧѓжЄЃКAEЃНDEЃЛ
ЃЈ2ЃЉШєAGЃН2ЃЌDGЃН4ЃЌЧѓAFЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЕуOЮЊзјБъдЕуЃЎвбжЊЗДБШР§КЏЪ§![]() ЕФЭМЯѓОAЃЈЉ2ЃЌmЃЉЃЌЙ§ЕузїABЁЭxжсЃЎДЙзуЮЊЕуBЃЌЧвЁїOABЕФУцЛ§ЮЊ1ЃЎ
ЕФЭМЯѓОAЃЈЉ2ЃЌmЃЉЃЌЙ§ЕузїABЁЭxжсЃЎДЙзуЮЊЕуBЃЌЧвЁїOABЕФУцЛ§ЮЊ1ЃЎ
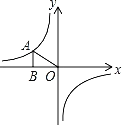
ЃЈ1ЃЉЧѓkКЭmЕФжЕЃЛ
ЃЈ2ЃЉЕуCЃЈxЃЌyЃЉдкЗДБШР§![]() ЕФЭМЯѓЩЯЃЌЕБ1ЁмxЁм3ЪБЃЌЧѓКЏЪ§жЕyЕФШЁжЕЗЖЮЇЃЎ
ЕФЭМЯѓЩЯЃЌЕБ1ЁмxЁм3ЪБЃЌЧѓКЏЪ§жЕyЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕФк, ![]() ЕФШ§ИіЖЅЕузјБъЗжБ№ЮЊ
ЕФШ§ИіЖЅЕузјБъЗжБ№ЮЊ![]() (2,-4)ЃЌ
(2,-4)ЃЌ ![]() (4,-4)ЃЌ
(4,-4)ЃЌ ![]() (1,-1).
(1,-1).

ЃЈ1ЃЉЛГі![]() Йигк
Йигк![]() жсЖдГЦЕФ
жсЖдГЦЕФ![]() ЃЌжБНгаДГіЕу
ЃЌжБНгаДГіЕу![]() ЕФзјБъЃЛ
ЕФзјБъЃЛ
ЃЈ2ЃЉЛГі![]() ШЦЕу
ШЦЕу![]() ФцЪБеыа§зЊ90ЁуКѓЕФ
ФцЪБеыа§зЊ90ЁуКѓЕФ![]() ЃЛ
ЃЛ
ЃЈ3ЃЉдк(2)ЕФЬѕМўЯТЃЌЧѓЯпЖЮ![]() ЩЈЙ§ЕФУцЛ§ЃЈНсЙћБЃСєІаЃЉ.
ЩЈЙ§ЕФУцЛ§ЃЈНсЙћБЃСєІаЃЉ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌЕуPЪЧБпГЄЮЊ2ЕФе§ЗНаЮABCDЕФЖдНЧЯпBDЩЯЕФЖЏЕуЃЌЙ§ЕуPЗжБ№зїPEЁЭBCгкЕуEЃЌPFЁЭDCгкЕуFЃЌСЌНгAPВЂбгГЄЃЌНЛЩфЯпBCгкЕуHЃЌНЛЩфЯпDCгкЕуMЃЌСЌНгEFНЛAHгкЕуGЃЌЕБЕуPдкBDЩЯдЫЖЏЪБЃЈВЛАќРЈBЁЂDСНЕуЃЉЃЌвдЯТНсТлжаЃКЂйMFЃНMCЃЛЂкAPЃНEFЃЛЂлAHЁЭEFЃЛЂмAP2ЃНPMPHЃЛЂнEFЕФзюаЁжЕЪЧ![]() ЃЎЦфжае§ШЗНсТлгаЃЈ ЃЉ
ЃЎЦфжае§ШЗНсТлгаЃЈ ЃЉ
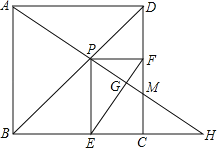
A.2ИіB.3ИіC.4ИіD.5Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЙ§дЕуOМАAЃЈ8ЃЌ0ЃЉЁЂCЃЈ0ЃЌ6ЃЉзїОиаЮOABCЃЌСЌНгACЃЌвЛИіжБНЧШ§НЧаЮPDEЕФжБНЧЖЅЕуPЪМжедкЖдНЧЯпACЩЯдЫЖЏЃЈВЛгыAЁЂCжиКЯЃЉЃЌЧвБЃГжвЛБпPDЪМжеОЙ§ОиаЮЖЅЕуBЃЌPEНЛxжсгкЕуQ
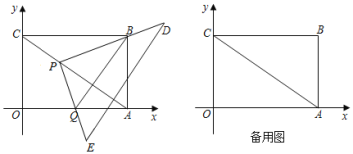
ЃЈ1ЃЉ![]() ЃН______ЃЛ
ЃН______ЃЛ
ЃЈ2ЃЉдкЕуPДгЕуCдЫЖЏЕНЕуAЕФЙ§ГЬжаЃЌ![]() ЕФжЕЪЧЗёЗЂЩњБфЛЏЃПШчЙћБфЛЏЃЌЧыЧѓГіЦфБфЛЏЗЖЮЇЃЌШчЙћВЛБфЃЌЧыЫЕУїРэгЩЃЌВЂЧѓГіЦфжЕЃЛ
ЕФжЕЪЧЗёЗЂЩњБфЛЏЃПШчЙћБфЛЏЃЌЧыЧѓГіЦфБфЛЏЗЖЮЇЃЌШчЙћВЛБфЃЌЧыЫЕУїРэгЩЃЌВЂЧѓГіЦфжЕЃЛ
ЃЈ3ЃЉШєНЋЁїQABбижБЯпBQелЕўКѓЃЌЕуAгыЕуPжиКЯЃЌдђPCЕФГЄЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПзлКЯгыЬНОП
ШчЭМЃЌХзЮяЯп![]() ОЙ§ЕуA(-2,0)ЃЌB(4,0)СНЕуЃЌгы
ОЙ§ЕуA(-2,0)ЃЌB(4,0)СНЕуЃЌгы![]() жсНЛгкЕуCЃЌЕуDЪЧХзЮяЯпЩЯвЛИіЖЏЕуЃЌЩшЕуDЕФКсзјБъЮЊ
жсНЛгкЕуCЃЌЕуDЪЧХзЮяЯпЩЯвЛИіЖЏЕуЃЌЩшЕуDЕФКсзјБъЮЊ![]() .СЌНгACЃЌBCЃЌDBЃЌDCЃЌ
.СЌНгACЃЌBCЃЌDBЃЌDCЃЌ
(1)ЧѓХзЮяЯпЕФКЏЪ§БэДяЪНЃЛ
(2)ЁїBCDЕФУцЛ§ЕШгкЁїAOCЕФУцЛ§ЕФ![]() ЪБЃЌЧѓ
ЪБЃЌЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
(3)дк(2)ЕФЬѕМўЯТЃЌШєЕуMЪЧ![]() жсЩЯЕФвЛИіЖЏЕуЃЌЕуNЪЧХзЮяЯпЩЯвЛЖЏЕуЃЌЪдХаЖЯЪЧЗёДцдкетбљЕФЕуM,ЪЙЕУвдЕуBЃЌDЃЌMЃЌNЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃЌШєДцдкЃЌЧыжБНгаДГіЕуMЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
жсЩЯЕФвЛИіЖЏЕуЃЌЕуNЪЧХзЮяЯпЩЯвЛЖЏЕуЃЌЪдХаЖЯЪЧЗёДцдкетбљЕФЕуM,ЪЙЕУвдЕуBЃЌDЃЌMЃЌNЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃЌШєДцдкЃЌЧыжБНгаДГіЕуMЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЩЬГЁОйАьГщНБЛюЖЏЃЌЙцдђШчЯТЃКдкВЛЭИУїЕФДќзгжага2ИіКьЧђКЭ2ИіКкЧђЃЌетаЉЧђГ§беЩЋЭтЖМЯрЭЌЃЌЙЫПЭУПДЮУўГівЛИіЧђЃЌШєУўЕНКьЧђЃЌдђЛёЕУ1ЗнНБЦЗЃЌШєУўЕНКкЧђЃЌдђУЛгаНБЦЗЁЃ
ЃЈ1ЃЉШчЙћаЁЗМжЛгавЛДЮУўЧђЛњЛсЃЌФЧУДаЁЗМЛёЕУНБЦЗЕФИХТЪЮЊ ЁЁЃЛ
ЃЈ2ЃЉШчЙћаЁЗМгаСНДЮУўЧђЛњЛсЃЈУўГіКѓВЛЗХЛиЃЉЃЌЧѓаЁЗМЛёЕУ2ЗнНБЦЗЕФИХТЪЁЃЃЈЧыгУЁАЛЪїзДЭМЁБЛђЁАСаБэЁБЕШЗНЗЈаДГіЗжЮіЙ§ГЬЃЉ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com