
ΓΨΧβΡΩΓΩΉέΚœ”κΧΫΨΩ
»γΆΦΘ§≈ΉΈοœΏ![]() Ψ≠ΙΐΒψA(-2,0)Θ§B(4,0)ΝΫΒψΘ§”κ
Ψ≠ΙΐΒψA(-2,0)Θ§B(4,0)ΝΫΒψΘ§”κ![]() ÷αΫΜ”ΎΒψCΘ§ΒψD «≈ΉΈοœΏ…œ“ΜΗωΕ·ΒψΘ§…ηΒψDΒΡΚαΉχ±ξΈΣ
÷αΫΜ”ΎΒψCΘ§ΒψD «≈ΉΈοœΏ…œ“ΜΗωΕ·ΒψΘ§…ηΒψDΒΡΚαΉχ±ξΈΣ![]() .Ν§Ϋ”ACΘ§BCΘ§DBΘ§DCΘ§
.ͧ۔ACȧBCȧDBȧDCȧ
(1)«σ≈ΉΈοœΏΒΡΚ· ΐ±μ¥ο ΫΘΜ
(2)ΓςBCDΒΡΟφΜΐΒ»”ΎΓςAOCΒΡΟφΜΐΒΡ![]() ±Θ§«σ
±Θ§«σ![]() ΒΡ÷ΒΘΜ
ΒΡ÷ΒΘΜ
(3)‘Ύ(2)ΒΡΧθΦΰœ¬Θ§»τΒψM «![]() ÷α…œΒΡ“ΜΗωΕ·ΒψΘ§ΒψN «≈ΉΈοœΏ…œ“ΜΕ·ΒψΘ§ ‘≈–Εœ «Ζώ¥φ‘Ύ’β―υΒΡΒψM, ΙΒΟ“‘ΒψBΘ§DΘ§MΘ§NΈΣΕΞΒψΒΡΥΡ±Ώ–Έ «ΤΫ––ΥΡ±Ώ–ΈΘ§»τ¥φ‘ΎΘ§«κ÷±Ϋ”–¥≥ωΒψMΒΡΉχ±ξΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”….
÷α…œΒΡ“ΜΗωΕ·ΒψΘ§ΒψN «≈ΉΈοœΏ…œ“ΜΕ·ΒψΘ§ ‘≈–Εœ «Ζώ¥φ‘Ύ’β―υΒΡΒψM, ΙΒΟ“‘ΒψBΘ§DΘ§MΘ§NΈΣΕΞΒψΒΡΥΡ±Ώ–Έ «ΤΫ––ΥΡ±Ώ–ΈΘ§»τ¥φ‘ΎΘ§«κ÷±Ϋ”–¥≥ωΒψMΒΡΉχ±ξΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”….

ΓΨ¥πΑΗΓΩ(1)![]() ΘΜ(2)3ΘΜ(3)
ΘΜ(2)3ΘΜ(3)![]() .
.
ΓΨΫβΈωΓΩ
(1)άϊ”Ο¥ΐΕ®œΒ ΐΖ®Ϋχ––«σΫβΦ¥Ω…ΘΜ
(2)Ής÷±œΏDEΓΆ![]() ÷α”ΎΒψEΘ§ΫΜBC”ΎΒψGΘ§ΉςCFΓΆDEΘ§¥ΙΉψΈΣFΘ§œ»«σ≥ωSΓςOAC=6Θ§‘ΌΗυΨίSΓςBCD=
÷α”ΎΒψEΘ§ΫΜBC”ΎΒψGΘ§ΉςCFΓΆDEΘ§¥ΙΉψΈΣFΘ§œ»«σ≥ωSΓςOAC=6Θ§‘ΌΗυΨίSΓςBCD=![]() SΓςAOCΘ§ΒΟΒΫSΓςBCD =
SΓςAOCΘ§ΒΟΒΫSΓςBCD =![]() Θ§»ΜΚσ«σ≥ωBCΒΡΫβΈω ΫΈΣ
Θ§»ΜΚσ«σ≥ωBCΒΡΫβΈω ΫΈΣ![]() Θ§‘ρΩ…ΒΟΒψGΒΡΉχ±ξΈΣ
Θ§‘ρΩ…ΒΟΒψGΒΡΉχ±ξΈΣ![]() Θ§”…¥ΥΩ…ΒΟ
Θ§”…¥ΥΩ…ΒΟ![]() Θ§‘ΌΗυΨίSΓςBCD=SΓςCDG+SΓςBDG=
Θ§‘ΌΗυΨίSΓςBCD=SΓςCDG+SΓςBDG=![]() Θ§Ω…ΒΟΙΊ”ΎmΒΡΖΫ≥ΧΘ§ΫβΖΫ≥ΧΦ¥Ω…«σΒΟ¥πΑΗΘΜ
Θ§Ω…ΒΟΙΊ”ΎmΒΡΖΫ≥ΧΘ§ΫβΖΫ≥ΧΦ¥Ω…«σΒΟ¥πΑΗΘΜ
(3)¥φ‘ΎΘ§»γœ¬ΆΦΥυ ΨΘ§“‘BDΈΣ±ΏΜρ’Ώ“‘BDΈΣΕ‘Ϋ«œΏΫχ––ΤΫ––ΥΡ±Ώ–ΈΒΡΙΙΆΦΘ§“‘BDΈΣ±Ώ ±Θ§”–3÷÷«ιΩωΘ§”…ΒψDΒΡΉχ±ξΩ…ΒΟΒψNΒψΉίΉχ±ξΈΣΓά![]() Θ§»ΜΚσΖ÷ΒψNΒΡΉίΉχ±ξΈΣ
Θ§»ΜΚσΖ÷ΒψNΒΡΉίΉχ±ξΈΣ![]() ΚΆΒψNΒΡΉίΉχ±ξΈΣ
ΚΆΒψNΒΡΉίΉχ±ξΈΣ![]() ΝΫ÷÷«ιΩωΖ÷±π«σΫβΘΜ“‘BDΈΣΕ‘Ϋ«œΏ ±Θ§”–1÷÷«ιΩωΘ§¥Υ ±N1Βψ”κN2Βψ÷ΊΚœΘ§ΗυΨίΤΫ––ΥΡ±Ώ–ΈΒΡΕ‘±ΏΤΫ––«“œύΒ»Ω…«σΒΟBM1=N1D=4Θ§ΦΧΕχ«σΒΟOM1= 8Θ§”…¥ΥΦ¥Ω…«σΒΟ¥πΑΗ.
ΝΫ÷÷«ιΩωΖ÷±π«σΫβΘΜ“‘BDΈΣΕ‘Ϋ«œΏ ±Θ§”–1÷÷«ιΩωΘ§¥Υ ±N1Βψ”κN2Βψ÷ΊΚœΘ§ΗυΨίΤΫ––ΥΡ±Ώ–ΈΒΡΕ‘±ΏΤΫ––«“œύΒ»Ω…«σΒΟBM1=N1D=4Θ§ΦΧΕχ«σΒΟOM1= 8Θ§”…¥ΥΦ¥Ω…«σΒΟ¥πΑΗ.
(1)≈ΉΈοœΏ![]() Ψ≠ΙΐΒψA(-2,0)Θ§B(4,0)Θ§
Ψ≠ΙΐΒψA(-2,0)Θ§B(4,0)Θ§
Γύ![]() Θ§
Θ§
ΫβΒΟ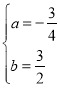 Θ§
Θ§
Γύ≈ΉΈοœΏΒΡΚ· ΐ±μ¥ο ΫΈΣ![]() ΘΜ
ΘΜ
(2)Ής÷±œΏDEΓΆ![]() ÷α”ΎΒψEΘ§ΫΜBC”ΎΒψGΘ§ΉςCFΓΆDEΘ§¥ΙΉψΈΣFΘ§
÷α”ΎΒψEΘ§ΫΜBC”ΎΒψGΘ§ΉςCFΓΆDEΘ§¥ΙΉψΈΣFΘ§
ΓΏΒψAΒΡΉχ±ξΈΣ(-2,0)Θ§ΓύOA=2Θ§
”…![]() Θ§ΒΟ
Θ§ΒΟ![]() Θ§ΓύΒψCΒΡΉχ±ξΈΣ(0,6)Θ§ΓύOC=6Θ§
Θ§ΓύΒψCΒΡΉχ±ξΈΣ(0,6)Θ§ΓύOC=6Θ§
ΓύSΓςOAC=![]() Θ§
Θ§
ΓΏSΓςBCD=![]() SΓςAOCΘ§
SΓςAOCΘ§
ΓύSΓςBCD =![]() Θ§
Θ§
…η÷±œΏBCΒΡΚ· ΐ±μ¥ο ΫΈΣ![]() Θ§
Θ§
”…BΘ§CΝΫΒψΒΡΉχ±ξΒΟ![]() Θ§ΫβΒΟ
Θ§ΫβΒΟ Θ§
Θ§
Γύ÷±œΏBCΒΡΚ· ΐ±μ¥ο ΫΈΣ![]() Θ§
Θ§
ΓύΒψGΒΡΉχ±ξΈΣ![]() Θ§
Θ§
Γύ![]() Θ§
Θ§
ΓΏΒψBΒΡΉχ±ξΈΣ(4,0)Θ§ΓύOB=4Θ§
ΓΏSΓςBCD=SΓςCDG+SΓςBDG=![]() Θ§
Θ§
ΓύSΓςBCD =![]() Θ§
Θ§
Γύ![]() Θ§
Θ§
ΫβΒΟ![]() (…α)Θ§
(…α)Θ§![]() Θ§
Θ§
Γύ![]() ΒΡ÷ΒΈΣ3ΘΜ
ΒΡ÷ΒΈΣ3ΘΜ
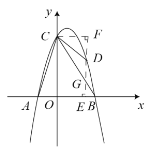
(3)¥φ‘ΎΘ§»γœ¬ΆΦΥυ ΨΘ§“‘BDΈΣ±ΏΜρ’Ώ“‘BDΈΣΕ‘Ϋ«œΏΫχ––ΤΫ––ΥΡ±Ώ–ΈΒΡΙΙΆΦΘ§
“‘BDΈΣ±Ώ ±Θ§”–3÷÷«ιΩωΘ§
ΓΏDΒψΉχ±ξΈΣ![]() Θ§ΓύΒψNΒψΉίΉχ±ξΈΣΓά
Θ§ΓύΒψNΒψΉίΉχ±ξΈΣΓά![]() Θ§
Θ§
Β±ΒψNΒΡΉίΉχ±ξΈΣ![]() ±Θ§»γΒψN2Θ§
±Θ§»γΒψN2Θ§
¥Υ ±![]() Θ§ΫβΒΟΘΚ
Θ§ΫβΒΟΘΚ![]() (…α)Θ§
(…α)Θ§
Γύ![]() Θ§Γύ
Θ§Γύ![]() ΘΜ
ΘΜ
Β±ΒψNΒΡΉίΉχ±ξΈΣ![]() ±Θ§»γΒψN3Θ§N4Θ§
±Θ§»γΒψN3Θ§N4Θ§
¥Υ ±![]() Θ§ΫβΒΟΘΚ
Θ§ΫβΒΟΘΚ![]()
Γύ![]() Θ§
Θ§![]() Θ§
Θ§
Γύ![]() Θ§
Θ§![]() ΘΜ
ΘΜ
“‘BDΈΣΕ‘Ϋ«œΏ ±Θ§”–1÷÷«ιΩωΘ§¥Υ ±N1Βψ”κN2Βψ÷ΊΚœΘ§
ΓΏ![]() Θ§D(3Θ§
Θ§D(3Θ§![]() )Θ§
)Θ§
ΓύN1D=4Θ§
ΓύBM1=N1D=4Θ§
ΓύOM1=OB+BM1=8Θ§
ΓύM1(8Θ§0)Θ§
Ήέ…œΘ§ΒψMΒΡΉχ±ξΈΣΘΚ![]() .
.



 Οϊ–ΘΩΈΧΟœΒΝ–¥πΑΗ
Οϊ–ΘΩΈΧΟœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΕΪΈςΖΫœρΒΡΚΘΑΕœΏ![]() ΝΫΥ“¥§Θ§Ψυ ’ΒΫ“―¥ΞΫΗΗι«≥ΒΡ¥§
ΝΫΥ“¥§Θ§Ψυ ’ΒΫ“―¥ΞΫΗΗι«≥ΒΡ¥§![]() ΒΡ«σΨ»–≈Κ≈Θ§“―÷Σ¥§
ΒΡ«σΨ»–≈Κ≈Θ§“―÷Σ¥§![]() ‘Ύ¥§
‘Ύ¥§![]() ΒΡ±±ΤΪΕΪ58ΓψΖΫœρΘ§¥§
ΒΡ±±ΤΪΕΪ58ΓψΖΫœρΘ§¥§![]() ‘Ύ¥§
‘Ύ¥§![]() ΒΡ±±ΤΪΈς35ΓψΖΫœρΘ§«“
ΒΡ±±ΤΪΈς35ΓψΖΫœρΘ§«“![]() ΒΡΨύάκΈΣ30ΚΘάο.Ιέ≤λΆΦ–Έ≤ΔΜΊ¥πΈ ΧβΘΚΘ®≤ΈΩΦ ΐΨίΘΚ
ΒΡΨύάκΈΣ30ΚΘάο.Ιέ≤λΆΦ–Έ≤ΔΜΊ¥πΈ ΧβΘΚΘ®≤ΈΩΦ ΐΨίΘΚ![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ©
Θ©
Θ®1Θ©«σ¥§![]() ΒΫΚΘΑΕœΏ
ΒΫΚΘΑΕœΏ![]() ΒΡΨύάκΘ®ΨΪ»ΖΒΫ0.1ΚΘάοΘ©ΘΜ
ΒΡΨύάκΘ®ΨΪ»ΖΒΫ0.1ΚΘάοΘ©ΘΜ
Θ®2Θ©»τ¥§![]() ΓΔ¥§
ΓΔ¥§![]() Ζ÷±π“‘20ΚΘάο/–Γ ±ΓΔ15ΚΘάο/–Γ ±ΒΡΥΌΕ»Ά§ ±≥ωΖΔΘ§‘»ΥΌ÷±œΏ«ΑΆυΨ»‘°Θ§ ‘Ά®ΙΐΦΤΥψ≈–ΕœΡΡΥ“¥§œ»Βۥ不
Ζ÷±π“‘20ΚΘάο/–Γ ±ΓΔ15ΚΘάο/–Γ ±ΒΡΥΌΕ»Ά§ ±≥ωΖΔΘ§‘»ΥΌ÷±œΏ«ΑΆυΨ»‘°Θ§ ‘Ά®ΙΐΦΤΥψ≈–ΕœΡΡΥ“¥§œ»Βۥ不![]() ¥Π.
¥Π.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΙΊ”ΎxΒΡ“Μ‘ΣΕΰ¥ΈΖΫ≥Χx2+2x©¹Θ®m©¹2Θ©ΘΫ0”– Β ΐΗυΘ°
Θ®1Θ©«σmΒΡ»Γ÷ΒΖΕΈßΘΜ
Θ®2Θ©»τΖΫ≥Χ”–“ΜΗωΗυΈΣxΘΫ1Θ§«σmΒΡ÷ΒΦΑΝμ“ΜΗωΗυΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
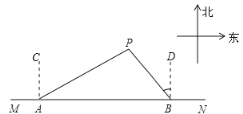
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§Εΰ¥ΈΚ· ΐΒΡΆΦœσΫΜΉχ±ξ÷α”ΎAΘ®©¹1Θ§0Θ©Θ§BΘ®4Θ§0Θ©Θ§CΘ®0Θ§©¹4Θ©»ΐΒψΘ§ΒψP «÷±œΏBCœ¬ΖΫ≈ΉΈοœΏ…œ“ΜΕ·ΒψΘ°
Θ®1Θ©«σ’βΗωΕΰ¥ΈΚ· ΐΒΡΫβΈω ΫΘΜ
Θ®2Θ© «Ζώ¥φ‘ΎΒψPΘ§ ΙΓςPOC «“‘OCΈΣΒΉ±ΏΒΡΒ»―ϋ»ΐΫ«–ΈΘΩ»τ¥φ‘ΎΘ§«σ≥ωPΒψΉχ±ξΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…ΘΜ
Θ®3Θ©Ε·ΒψP‘ΥΕ·ΒΫ ≤Ο¥ΈΜ÷Ο ±Θ§ΓςPBCΟφΜΐΉν¥σΘ§«σ≥ω¥Υ ±PΒψΉχ±ξΚΆΓςPBCΒΡΉν¥σΟφΜΐΘ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§≈ΉΈοœΏ![]() ”κ
”κ![]() ÷αΫΜ”Ύ
÷αΫΜ”Ύ![]() ΓΔ
ΓΔ![]() ΝΫΒψΘ§
ΝΫΒψΘ§![]() «“‘Βψ
«“‘Βψ![]() Θ®0,3Θ©ΈΣ‘≤–ΡΘ§2ΈΣΑκΨΕΒΡ‘≤…œΒΡΕ·ΒψΘ§
Θ®0,3Θ©ΈΣ‘≤–ΡΘ§2ΈΣΑκΨΕΒΡ‘≤…œΒΡΕ·ΒψΘ§![]() «œΏΕΈ
«œΏΕΈ![]() ΒΡ÷–ΒψΘ§Ν§Ϋα
ΒΡ÷–ΒψΘ§Ν§Ϋα![]() .‘ρœΏΕΈ
.‘ρœΏΕΈ![]() ΒΡΉν¥σ÷Β «Θ® Θ©
ΒΡΉν¥σ÷Β «Θ® Θ©
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
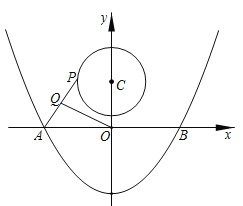
ΓΨΧβΡΩΓΩ»γΆΦΘ§Ζ¥±»άΐΚ· ΐyΘΫ![]() (xΘΨ0)ΒΡΆΦœσΨ≠ΙΐΨΊ–ΈOABCΕ‘Ϋ«œΏΒΡΫΜΒψMΘ§Ζ÷±π”κABΓΔBCœύΫΜ”ΎΒψDΓΔEΘ°»τΥΡ±Ώ–ΈODBEΒΡΟφΜΐΈΣ9Θ§‘ρkΒΡ÷ΒΈΣΘ® Θ©
(xΘΨ0)ΒΡΆΦœσΨ≠ΙΐΨΊ–ΈOABCΕ‘Ϋ«œΏΒΡΫΜΒψMΘ§Ζ÷±π”κABΓΔBCœύΫΜ”ΎΒψDΓΔEΘ°»τΥΡ±Ώ–ΈODBEΒΡΟφΜΐΈΣ9Θ§‘ρkΒΡ÷ΒΈΣΘ® Θ©
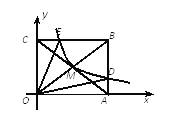
A. 3B. 6C. 9D. 4
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥ΧθΒά¬Ζ…œΆ®––≥ΒΝΨœόΥΌ60«ßΟΉ/ ±Θ§Βά¬ΖΒΡABΕΈΈΣΦύ≤β«χΘ§Φύ≤βΒψPΒΫABΒΡΨύάκPHΈΣ50ΟΉΘ®»γΆΦΘ©Θ°“―÷ΣΒψP‘ΎΒψAΒΡ±±ΤΪΕΪ45ΓψΖΫœρ…œΘ§«“‘ΎΒψBΒΡ±±ΤΪΈς60ΓψΖΫœρ…œΘ§ΒψB‘ΎΒψAΒΡ±±ΤΪΕΪ75ΓψΖΫœρ…œΘ§Ρ«Ο¥≥ΒΝΨΆ®ΙΐABΕΈΒΡ ±Φδ‘ΎΕύ…ΌΟκ“‘ΡΎΘ§Ω…»œΕ®ΈΣ≥§ΥΌΘΩΘ®≤ΈΩΦ ΐΨίΘΚ![]() Γ÷1.7Θ§
Γ÷1.7Θ§![]() Γ÷1.4Θ©Θ°
Γ÷1.4Θ©Θ°
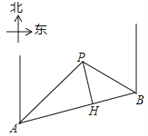
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§RtΓςABC÷–Θ§ABΓΆBCΘ§AB=6Θ§BC=4Θ§P «ΓςABCΡΎ≤ΩΒΡ“ΜΗωΕ·ΒψΘ§«“¬ζΉψΓœPAB=ΓœPBCΘ§‘ρœΏΕΈCP≥ΛΒΡΉν–Γ÷ΒΈΣΘ®ΓΓΓΓΘ©
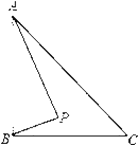
A. 2 B. ![]() C.
C. ![]() D.
D. ![]()
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦ1Θ§‘ΎΓςABC÷–Θ§ΒψPΈΣBC±Ώ…œ“ΜΒψΘ§…ηBPΘΫxΘ§AP2ΘΫyΘ§“―÷Σy «xΒΡΕΰ¥ΈΚ· ΐΒΡ“Μ≤ΩΖ÷Θ§ΤδΆΦœσ»γΆΦ2Θ§ΒψQΘ®2Θ§12Θ© «ΆΦœσ…œΒΡΉνΒΆΒψΘ§«“ΆΦœσ”κy÷αΫΜ”ΎΘ®0Θ§16Θ©Θ°
Θ®1Θ©«σyΙΊ”ΎxΒΡΚ· ΐΫβΈω ΫΘΜ
Θ®2Θ©Β±ΓςABPΈΣ÷±Ϋ«»ΐΫ«–Έ ±Θ§BPΒΡ÷Β «Εύ…ΌΘΩ
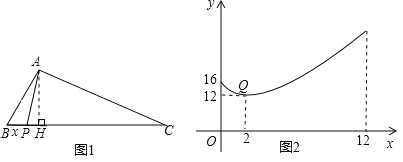
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com