
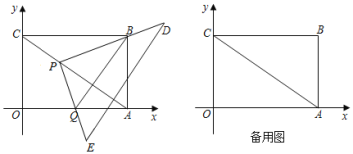
【题目】如图,在平面直角坐标系中,过原点O及A(8,0)、C(0,6)作矩形OABC,连接AC,一个直角三角形PDE的直角顶点P始终在对角线AC上运动(不与A、C重合),且保持一边PD始终经过矩形顶点B,PE交x轴于点Q
(1)![]() =______;
=______;
(2)在点P从点C运动到点A的过程中,![]() 的值是否发生变化?如果变化,请求出其变化范围,如果不变,请说明理由,并求出其值;
的值是否发生变化?如果变化,请求出其变化范围,如果不变,请说明理由,并求出其值;
(3)若将△QAB沿直线BQ折叠后,点A与点P重合,则PC的长为_____.
【答案】(1)![]() ;(2)
;(2)![]() 的值不发生变化,
的值不发生变化,![]() =
=![]() ,理由见解析;(3)2.8.
,理由见解析;(3)2.8.
【解析】
(1)根据A、C两点坐标可得OA、OC的长,根据矩形的性质可得AB=OC、BC=OA,即可得答案;(2)由∠OAB=∠BPQ=90°,根据四边形内角和可得∠AOB+∠BPQ=180°,可得A、B、P、Q四点共圆,根据圆周角定理可得∠PQB=∠PAB,即可证明△PBQ∽△BCA,根据相似三角形的性质可得![]() =
=![]() =
=![]() ,即可得答案;(3)设BQ交AP于M,利用勾股定理可得AC=10,根据折叠性质可得BQ⊥AP,PM=AM,即可证明△ABM∽△ACB,根据相似三角形的性质可求出AM的长,进而求出PC的长即可.
,即可得答案;(3)设BQ交AP于M,利用勾股定理可得AC=10,根据折叠性质可得BQ⊥AP,PM=AM,即可证明△ABM∽△ACB,根据相似三角形的性质可求出AM的长,进而求出PC的长即可.
(1)∵A(8,0)、C(0,6),
∴OA=8,OC=6,
∵四边形OABC是矩形,
∴∠ABC=∠OAB=90°,BC=OA=8,AB=OC=6,
∴![]() =
=![]() =
=![]() ,
,
故答案为:![]()
(2)![]() 的值不发生变化,
的值不发生变化,![]() =
=![]() ,理由如下:
,理由如下:
∵∠OAB=∠BPQ=90°,
∴∠PQA+∠ABP=180°,
∴A、B、P、Q四点共圆,
∴∠PQB=∠PAB,
∵∠ABC=∠BPQ=90°,
∴△PBQ∽△BCA,
∴![]() =
=![]() =
=![]() .
.
∴![]() 的值不发生变化,
的值不发生变化,![]() =
=![]() .
.
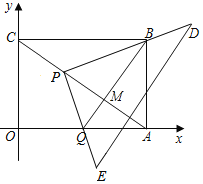
(3)设BQ交AP于M,如图所示:
在Rt△ABC中,由勾股定理得:AC=![]() =
=![]() =10,
=10,
由折叠的性质得:BQ⊥AP,PM=AM,
∴∠AMB=90°=∠ABC,
∵∠BAM=∠CAB,
∴△ABM∽△ACB,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得:AM=3.6,
∴PA=2AM=7.2,
∴PC=AC﹣PA=10﹣7.2=2.8,
故答案为:2.8


科目:初中数学 来源: 题型:
【题目】已知BD是矩形ABCD的对角线,AB=20厘米,BC=40厘米.点P、Q同时从点A出发,分别以2厘米/秒、4厘米/秒的速度由A→B→C→D→A的方向在矩形边上运动,只要Q点回到点A,运动全部停止.设运动时间为t秒.
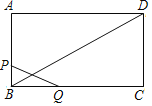
(1)当点P运动在AB(含B点)上,点Q运动在BC(含B、C点)上时,
①设PQ的长为y,求y关于时间t的函数关系式,并写出t的取值范围?
②当t为何值时,△DPQ是等腰三角形?
(2)在P、Q的整个运动过程中,分别判断下列两种情形是否存在?如果存在,请求出t的值;如果不存在,请说明理由.
①PQ与BD平行;
②PQ与BD垂直.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年12月4日是第五个国家宪法日,也是第一个“宪法宣传周”.甲、乙两班各选派10名学生参加宪法知识竞赛(满分100分),成绩如下:
成绩 | 85 | 90 | 95 | 100 |
甲班参赛学生/人 | 1 | 1 | 5 | 3 |
乙班参赛学生/人 | 1 | 2 | 3 | 4 |
分别求甲、乙两班参赛学生竞赛成绩的平均数和方差.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线经过点A(﹣1,0),B(4,0),C(0,2)三点,点D与点C关于x轴对称,点P是线段AB上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线l交抛物线于点Q,交直线BD于点M.
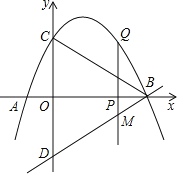
(1)求该抛物线所表示的二次函数的表达式;
(2)求证:∠ACB=90°;
(3)在点P运动过程中,是否存在点Q,使得△BQM是直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由;
(4)连接AC,将△AOC绕平面内某点H顺时针旋转90°,得到△A1O1C1,点A、O、C的对应点分别是点A1、O1、C1、若△A1O1C1的两个顶点恰好落在抛物线上,那么我们就称这样的点为“和谐点”,请直接写出“和谐点”的个数和点A1的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为纪念建国70周年,某校举行班级歌咏比赛,歌曲有:《我爱你,中国》,《歌唱祖国》,《我和我的祖国》(分别用字母A,B,C依次表示这三首歌曲).比赛时,将A,B,C这三个字母分别写在3张无差别不透明的卡片正面上,洗匀后正面向下放在桌面上,八(1)班班长先从中随机抽取一张卡片,放回后洗匀,再由八(2)班班长从中随机抽取一张卡片,进行歌咏比赛.
(1)八(1)班抽中歌曲《我和我的祖国》的概率是__________;
(2)试用画树状图或列表的方法表示所有可能的结果,并求出八(1)班和八(2)班抽中不同歌曲的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,梯形ABCD中,AB//CD,且AB=2CD,E,F分别是AB,BC的中点.
EF与BD相交于点M.

(1)求证:△EDM∽△FBM;
(2)若DB=9,求BM.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
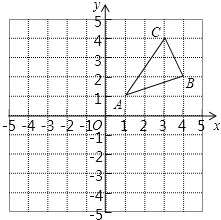
(1)请画出△ABC向下平移6个单位得到的△A1B1C1,并写出A1的坐标;
(2)请画出△ABC关于原点对称的△A2B2C2,并写出点B2的坐标;
(3)分别连接B2C和C2B,判断四边形CBC2B2是什么特殊的四边形(不用说明理由);
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于下列说法:(1)反比例函数![]() ,在每个象限内
,在每个象限内![]() 随
随![]() 的增大而减小;(2)函数
的增大而减小;(2)函数![]() ,
,![]() 随
随![]() 的增大减小;(3)函数
的增大减小;(3)函数![]() ,当
,当![]() 时,
时,![]() 随
随![]() 的增大而减小,其中正确的有( )
的增大而减小,其中正确的有( )
A.0个B.1个C.2个D.3个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com