【题目】如图，△ABC三个顶点的坐标分别为A（1，1），B（4，2），C（3，4）．
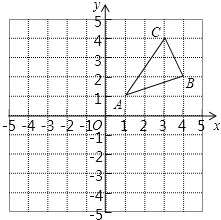
（1）请画出△ABC向下平移6个单位得到的△A1B1C1，并写出A1的坐标；
（2）请画出△ABC关于原点对称的△A2B2C2，并写出点B2的坐标；
（3）分别连接B2C和C2B，判断四边形CBC2B2是什么特殊的四边形（不用说明理由）；
寒假创新型自主学习第三学期寒假衔接系列答案科目：初中数学 来源： 题型：
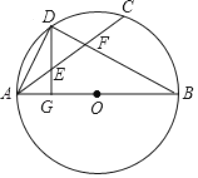
【题目】如图，AB为⊙O直径，D为弧AC的中点，DG⊥AB于G，交AC于E，AC、BD相交于F．
（1）求证：AE＝DE；
（2）若AG＝2，DG＝4，求AF的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，过原点O及A（8，0）、C（0，6）作矩形OABC，连接AC，一个直角三角形PDE的直角顶点P始终在对角线AC上运动（不与A、C重合），且保持一边PD始终经过矩形顶点B，PE交x轴于点Q
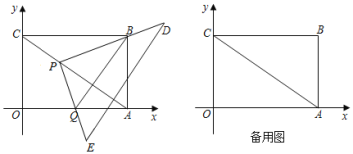
（1）
＝______；
（2）在点P从点C运动到点A的过程中，
的值是否发生变化？如果变化，请求出其变化范围，如果不变，请说明理由，并求出其值；
（3）若将△QAB沿直线BQ折叠后，点A与点P重合，则PC的长为_____．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】综合与探究
如图，抛物线
经过点A(-2,0)，B(4,0)两点，与
轴交于点C，点D是抛物线上一个动点，设点D的横坐标为
.连接AC，BC，DB，DC，
(1)求抛物线的函数表达式；
(2)△BCD的面积等于△AOC的面积的
时，求
的值；
(3)在(2)的条件下，若点M是
轴上的一个动点，点N是抛物线上一动点，试判断是否存在这样的点M,使得以点B，D，M，N为顶点的四边形是平行四边形，若存在，请直接写出点M的坐标；若不存在，请说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某商店销售一种商品，童威经市场调查发现：该商品的周销售量
（件）是售价
（元/件）的一次函数，其售价、周销售量、周销售利润
（元）的三组对应值如下表：
售价 | 50 | 60 | 80 |
周销售量 | 100 | 80 | 40 |
周销售利润 | 1000 | 1600 | 1600 |
注：周销售利润＝周销售量×（售价－进价）
（1）①求关于的函数解析式（不要求写出自变量的取值范围）
②该商品进价是_________元/件；当售价是________元/件时，周销售利润最大，最大利润是__________元
（2）由于某种原因，该商品进价提高了
元/件
，物价部门规定该商品售价不得超过65元/件，该商店在今后的销售中，周销售量与售价仍然满足（1）中的函数关系．若周销售最大利润是1400元，求的值
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系xOy中，一次函数y＝﹣2x的图象与反比例函数y＝
的图象的一个交点为A(﹣1，n)
(1)求反比例函数y＝的表达式.
(2)若两函数图象的另一交点为B，直接写出B的坐标.
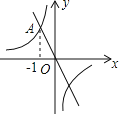
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知抛物线y=-x2+4x+5．
(1)用配方法将y=-x2+4x+5化成y=a（x﹣h）2+k的形式；
(2)指出抛物线的开口方向、对称轴和顶点坐标；
(3)若抛物线上有两点A（x1,y1）,B(x2,y2),如果x1>x2>2,试比较y1与y2的大小.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某商场举办抽奖活动，规则如下：在不透明的袋子中有2个红球和2个黑球，这些球除颜色外都相同，顾客每次摸出一个球，若摸到红球，则获得1份奖品，若摸到黑球，则没有奖品。
（1）如果小芳只有一次摸球机会，那么小芳获得奖品的概率为 ；
（2）如果小芳有两次摸球机会（摸出后不放回），求小芳获得2份奖品的概率。（请用“画树状图”或“列表”等方法写出分析过程）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系中，点
为坐标原点，抛物线
与
轴交于
、
两点，顶点
在
轴的正半轴上，且
．
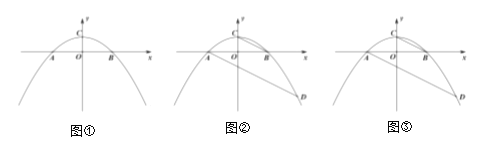
（1）如图①，求抛物线的解析式；
（2）如图②，连接
，过点作的平行线，交第四象限的抛物线于点
，求点的坐标；
（3）在（2）的条件下，点
在第四象限的抛物线上，过点作
于点
，直线
交轴于点
，过点作轴的垂线，垂足为
，点
在
的延长线上，连接
、
，且
，若
，求点的坐标．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
