
【题目】在平面直角坐标系中,点![]() 为坐标原点,抛物线
为坐标原点,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,顶点
两点,顶点![]() 在
在![]() 轴的正半轴上,且
轴的正半轴上,且![]() .
.
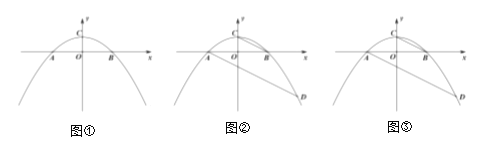
(1)如图①,求抛物线的解析式;
(2)如图②,连接![]() ,过点
,过点![]() 作
作![]() 的平行线,交第四象限的抛物线于点
的平行线,交第四象限的抛物线于点![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)在(2)的条件下,点![]() 在第四象限的抛物线上,过点
在第四象限的抛物线上,过点![]() 作
作![]() 于点
于点![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,点
,点![]() 在
在![]() 的延长线上,连接
的延长线上,连接![]() 、
、![]() ,且
,且![]() ,若
,若![]() ,求点
,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)点D的坐标为(4,
;(2)点D的坐标为(4,![]() );(3)点K的坐标为:(3,1)或(3,2).
);(3)点K的坐标为:(3,1)或(3,2).
【解析】
(1)根据题意,设点C坐标为(0,4a),由![]() ,求出A、B两点坐标,利用待定系数法即可解决问题;
,求出A、B两点坐标,利用待定系数法即可解决问题;
(2)先求出直线BC的解析式,由AD∥BC,得到k相等,再把点A代入,得到直线AD的方程,然后与二次函数组成方程组,即可得到点D的坐标;
(3)根据题意,过点F作FL⊥x轴于L,根据平面直角坐标系中的解直角三角形,结合条件![]() ,得到边之间的关系,设点E为(m,
,得到边之间的关系,设点E为(m,![]() ),则HE=
),则HE=![]() ,OH=m,利用边之间的关系建立关于m的一元二次方程,即可求出m的值,即得到点K的横坐标,由
,OH=m,利用边之间的关系建立关于m的一元二次方程,即可求出m的值,即得到点K的横坐标,由![]() ,需进行分类讨论,即可得到答案.
,需进行分类讨论,即可得到答案.
解:(1)如图①,
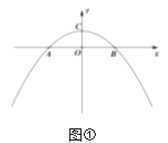
在![]() 中,设顶点C坐标为(0,4a),则OC=4a,
中,设顶点C坐标为(0,4a),则OC=4a,
∵![]() ,
,
∴OA=OB=2OC=8a,
∴点A坐标为(-8a,0),点B坐标为(8a,0),
把点B代入抛物线,得:![]() ,
,
解得:![]() 或
或![]() 或
或![]() ,
,
∵![]() ,则
,则![]() ,
,
∴![]() ,
,
∴抛物线的解析式为:![]() ;
;
(2)如图②,连接![]() ,过点
,过点![]() 作
作![]() 的平行线,交第四象限的抛物线于点
的平行线,交第四象限的抛物线于点![]() ,
,
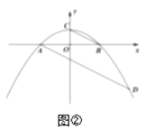
由(1)知,抛物线为![]() ,
,
∴点C坐标为(0,1),点B为(2,0),点A为(![]() ,0),
,0),
设直线BC的解析式为![]() ,
,
∴![]() ,解得:
,解得: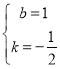 ,
,
∴直线BC的解析式为:![]() ;
;
∵AD∥BC,
∴设直线AD的解析式为![]() ,
,
把点A代入,得:![]() ,
,
∴![]() ,
,
∴直线AD的解析式为:![]() ;
;
∴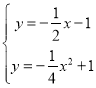 ,解得:
,解得: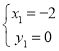 或
或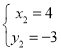 ,
,
∴点D的坐标为:(4,![]() );
);
(3)如图,过点F作FL⊥x轴于L,
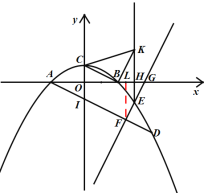
由(2)可知,直线AD为![]() ,
,
∴点I的坐标为:(0,![]() ),
),
∴OI=1,OA=2,
∴![]() .
.
∵FL⊥x轴,EH⊥x轴,EF⊥AD,
∴∠OAI+∠AGF=∠GEH+∠AGF=∠GFH+∠AGF=90°,
∴∠OAI =∠GEH=∠GFH,
∴![]() ,
,
即![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
即![]() ,
,
∴![]() ;
;
∴![]() ,
,
设点E坐标为(m,![]() ),
),
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴ ![]() ,
,
整理得:![]() ,
,
解得:![]() 或
或![]() (舍去);
(舍去);
∴点E的坐标为:(3,![]() );
);
∴点H为(3,0),点K的横坐标为3,
∴BH=1=OC,
①当CK平行x轴时,∠HBK=∠BKC=45°,
此时△BHK是等腰直角三角形,
∴HK=BK=1,
∴点K的坐标为(3,1);
②当△BKC时等腰直角三角形时,∠BKC=45°,则BC=BK,
∴△OBC≌△HKC(HL),
∴HK=OB=2,
∴点K的坐标为(3,2);
综合上述,点K的坐标为:(3,1)或(3,2).


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
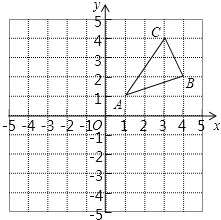
(1)请画出△ABC向下平移6个单位得到的△A1B1C1,并写出A1的坐标;
(2)请画出△ABC关于原点对称的△A2B2C2,并写出点B2的坐标;
(3)分别连接B2C和C2B,判断四边形CBC2B2是什么特殊的四边形(不用说明理由);
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于下列说法:(1)反比例函数![]() ,在每个象限内
,在每个象限内![]() 随
随![]() 的增大而减小;(2)函数
的增大而减小;(2)函数![]() ,
,![]() 随
随![]() 的增大减小;(3)函数
的增大减小;(3)函数![]() ,当
,当![]() 时,
时,![]() 随
随![]() 的增大而减小,其中正确的有( )
的增大而减小,其中正确的有( )
A.0个B.1个C.2个D.3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某反比例函数图象的一支经过点A(2,3)和点B(点B在点A的右侧),作BC⊥y轴,垂足为点C,连结AB,AC.
(1)求该反比例函数的解析式;
(2)若△ABC的面积为6,求直线AB的表达式.
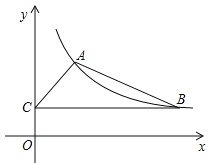
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在每个小正方形的边长均为1的方格纸中,其中端点![]() 、
、![]() 均在小正方形的顶点上.
均在小正方形的顶点上.
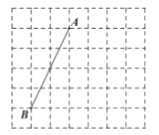
(1)在图中画出平行四边形![]() ,点
,点![]() 和点
和点![]() 均在小正方形的顶点上,且平行四边形
均在小正方形的顶点上,且平行四边形![]() 的面积为12;
的面积为12;
(2)在图中画出以![]() 为腰的等腰直角
为腰的等腰直角![]() ,且点
,且点![]() 在小正方形的顶点上;
在小正方形的顶点上;
(3)连接![]() ,直接写出
,直接写出![]() 的正切值.
的正切值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形![]() 是正方形,
是正方形,![]() 是等边三角形,
是等边三角形,![]() 为对角线
为对角线![]() (不含
(不含![]() 点)上任意一点,将
点)上任意一点,将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,连接
,连接![]() 、
、![]() 、
、![]() .设点
.设点![]() 的坐标为
的坐标为![]() .
.
(1)若建立平面直角坐标系,满足原点在线段![]() 上,点
上,点![]() ,
,![]() .且
.且![]() (
(![]() ),则点
),则点![]() 的坐标为 ,点
的坐标为 ,点![]() 的坐标为 ;请直接写出点
的坐标为 ;请直接写出点![]() 纵坐标
纵坐标![]() 的取值范围是 ;
的取值范围是 ;
(2)若正方形的边长为2,求![]() 的长,以及
的长,以及![]() 的最小值. (提示:连结
的最小值. (提示:连结![]() :
:![]() ,
,![]() )
)
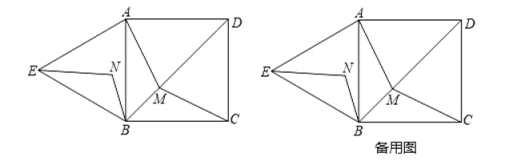
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,若![]() 是正数,直线
是正数,直线![]() :
:![]() 与
与![]() 轴交于点
轴交于点![]() ;直线
;直线![]() :
:![]() 与
与![]() 轴交于点
轴交于点![]() ;抛物线
;抛物线![]() :
:![]() 的顶点为
的顶点为![]() ,且
,且![]() 与
与![]() 轴右交点为
轴右交点为![]() .
.
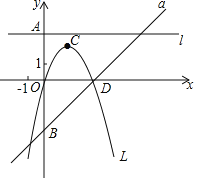
(1)若![]() ,求
,求![]() 的值,并求此时
的值,并求此时![]() 的对称轴与
的对称轴与![]() 的交点坐标;
的交点坐标;
(2)当点![]() 在
在![]() 下方时,求点
下方时,求点![]() 与
与![]() 距离的最大值;
距离的最大值;
(3)设![]() ,点
,点![]() ,
,![]() ,
,![]() 分别在
分别在![]() ,
,![]() 和
和![]() 上,且
上,且![]() 是
是![]() ,
,![]() 的平均数,求点
的平均数,求点![]() 与点
与点![]() 间的距离;
间的距离;
(4)在![]() 和
和![]() 所围成的封闭图形的边界上,把横、纵坐标都是整数的点称为“美点”,分别直接写出
所围成的封闭图形的边界上,把横、纵坐标都是整数的点称为“美点”,分别直接写出![]() 和
和![]() 时“美点”的个数.
时“美点”的个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
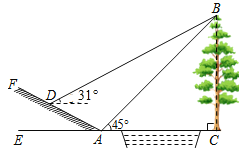
【题目】如图,小明为了测量小河对岸大树BC的高度,他在点A测得大树顶端B的仰角是45°,沿斜坡走![]() 米到达斜坡上点D,在此处测得树顶端点B的仰角为31°,且斜坡AF的坡比为1:2(参考数据:sin31°≈0.52,cos31°≈0.86,tan31°≈0.60).
米到达斜坡上点D,在此处测得树顶端点B的仰角为31°,且斜坡AF的坡比为1:2(参考数据:sin31°≈0.52,cos31°≈0.86,tan31°≈0.60).
(1)求小明从点A走到点D的过程中,他上升的高度;
(2)大树BC的高度约为多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
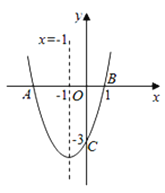
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A、B两点,与y轴交于点C,对称轴为直线x=-1,点B的坐标为(1,0),则下列结论:①AB=4;②b2-4ac>0;③ab<0;④a2-ab+ac<0,其中正确的结论有( )个.
A. 3B. 4C. 2D. 1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com